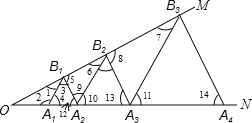
【题目】如图,已知:![]() ,点
,点![]() ……在射线ON上,点
……在射线ON上,点![]() ……在射线OM上,△
……在射线OM上,△![]() 、△
、△![]() 、△
、△![]() ……均为等边三角形,若
……均为等边三角形,若![]() ,则△
,则△![]() 的边长为( )
的边长为( )

A. 6 B. 12 C. 32 D. 64
参考答案:
【答案】C
【解析】试题解析:如图,∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°-120°-30°=30°,
又∵∠3=60°,
∴∠5=180°-60°-30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
…
∴△AnBnAn+1的边长为 2n-1,
∴△A6B6A7的边长为26-1=25=32.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为
 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
【答案】(1)证明见解析;(2)

【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得
 ≌
≌ 即可得
即可得 ,则可证得
,则可证得 为
为 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得 利用勾股定理即可求得
利用勾股定理即可求得 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得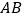 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得 与
与 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
∴ED⊥OD,
∴ED是
 的切线;
的切线;(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,

∵OE∥AB,
∴△COE∽△CAB,
 ∴AB=5,
∴AB=5,∵AC是直径,




∵EF∥AB,



∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为


【题型】解答题
【结束】
25【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数 y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线 x=1,下列结论:①ab<0;②b2>4ac;③a+b+2c<0;④3a+c<0.其中正确的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)

起点
A
B
C
D
终点
上车的人数
18
15
12
7
5
0
下车的人数
0
-3
-4
-10
-11
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图①,数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如,线段AB=0﹣(﹣1)=1:线段:BC=2﹣0=2;线段AC=2﹣(﹣1)=3(大的数减去小的数).
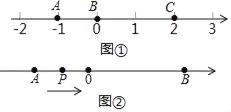
(1)数轴上点A、B表示的数分别是﹣3和2,则AB= ;
(2)数轴上点M表示的数是﹣1,线段MN的长为2,则点N表示的数是 ;
(3)如图②,数轴上点A、B表示的数分别是﹣4和6,动点P从点A出发,沿AB方向以每秒2个单位长度的速度运动,点P运动多少秒时BP=4.并求此时点P表示的数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为体现社会对教师的尊重,9月10日教师节这一天上午,出租车司机小军从红星出租车公司出发在东西向的公路上免费接送老师,如果规定向东为正,向西为负,出租车的连续行程如下(单位:千米):
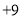 ,
,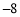 ,
,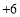 ,
,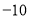 ,
,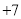 ,
,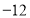 ,
,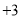 ,
,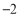 .(假定每次只接送一位老师,并且车上始终只有一位老师)
.(假定每次只接送一位老师,并且车上始终只有一位老师)(1)最后一名老师送到目的地时,小军在什么位置?
(2)离出发点最远的这位老师在什么位置?
(3)若汽车耗油量为0.3升/千米,这天上午汽车共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮参加中华诗词大赛,还剩最后两题,如果都答对,就可顺利通关.其中第一道单选题有4个选项,第二道单选题有3个选项.小亮这两道题都不会,不过还有一个“求助”没有使用(使用求助可以让主持人去掉其中一题的一个错误选项).
(1)如果小亮第一题使用“求助”,那么他答对第一道题的概率是__;
(2)他的亲友团建议:最后一题使用“求助”,从提高通关的可能性的角度看,你同意亲友团的观点吗?试说明理由.
相关试题

