【题目】如图,完成下列推理,并填写理由,如图,∠B=∠D,∠1=∠2,求证:AB∥CD. 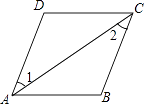
【证明】∵∠1=∠2(已知),
∴∥()
∴∠DAB+∠=180°()
∵∠B=∠D(已知)
∴∠DAB+∠=180°()
∴AB∥CD.
参考答案:
【答案】AD;BC;内错角相等两直线平行;B;两直线平行,同旁内角互补;D;等量代换
【解析】证明:∵∠1=∠2(已知), ∴AD∥BC(内错角相等,两直线平行),
∴∠DAB+∠B=180°(两直线平行,同旁内角互补),
∵∠B=∠D(已知),
∴∠DAB+∠D=180°(等量代换),
∴AB∥CD,
所以答案是:AD,BC,内错角相等两直线平行,B,两直线平行,同旁内角互补,D,等量代换.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个三角形的第一条边长为2a+5b,第二条边比第一条边长3a﹣2b,第三条边比第二条边短3a.
(1)则第二边的边长为 ,第三边的边长为 ;
(2)用含a,b的式子表示这个三角形的周长,并化简;
(3)若a,b满足|a﹣5|+(b﹣3)2=0,求出这个三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学小组的10位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数的2倍加1,第1位同学报(
 +1),第2位同学报(
+1),第2位同学报(  +1),第3位同学报(
+1),第3位同学报(  +1)…这样得到的n个数的积为 .
+1)…这样得到的n个数的积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4cm,AD=12cm,P点在AD边上以每秒1cm的速度从A向D运动,点Q在BC边上,以每秒4cm的速度从C点出发,在CB间往返运动,二点同时出发,待P点到达D点为止,在这段时间内,线段PQ有( )次平行于AB.

A.1 B.2 C.3 D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x﹣4=2﹣5x; (2)﹣(x﹣3)=3(2﹣5x);
(3)4x﹣2(
 ﹣x)=1; (4)
﹣x)=1; (4)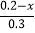 ﹣1=
﹣1=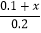 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】用
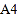 纸在某誊印社复印文件,复印页数不超过
纸在某誊印社复印文件,复印页数不超过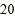 时每页收费
时每页收费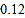 元;复印页数超过
元;复印页数超过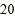 时,超过部分每页收费
时,超过部分每页收费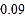 元.在某图书馆复印同样的文件,不论复印多少页,每页收费
元.在某图书馆复印同样的文件,不论复印多少页,每页收费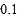 元,如何根据复印的页数选择复印的地点使总价格比较便宜?
元,如何根据复印的页数选择复印的地点使总价格比较便宜? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,AD=
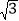 ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED。正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED。正确的是( )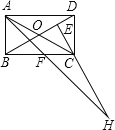
A. ②③ B. ②③④ C. ③④ D. ①②③④
相关试题

