【题目】小明家(记为A)、他上学的学校(记为B)、书店(记为C)依次坐落在一条东西走向的大街上,小明家位于学校西边250米处,书店位于学校东边100米处,小明中午放学后,到书店买本辅导书,然后回家吃中午饭,下午直接去学校上课.
(1)试用数轴表示出小明家(A)、学校(B)、书店(C)的位置;
(2)计算出小明家与书店的距离;
(3)小明从中午放学离校到下午上学到校一共走了多少米?
参考答案:
【答案】(1)见解析;(2)350米;(3)700米.
【解析】(1)根据题意,可设从西向东方向为正方向,学校所在位置为原点,则很容易用数轴来表示A、B、C的位置;
(2)根据(1)中的数轴回答问题;
(3)利用所走的路程求得绝对值的和即可.
(1)根据题意,可设从西向东方向为正方向,学校所在位置为原点,
则用数轴表示上述A、B、C的位置如下:
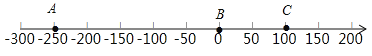
(2)由(1)中的数轴知,小明家与书店的距离100﹣(﹣250)=350米;
(3)从中午放学离校到下午上学到校一共走了100+100+250+250=700米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程:
计算:(-5)÷
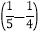 ×20.
×20.解:原式=(-5)÷
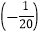 ×20 (第一步)
×20 (第一步)=(-5)÷(-1) (第二步)
=-5. (第三步)
(1)上述解题过程中有两处错误:
第一处是第________步,错误的原因是__________________________;
第二处是第________步,错误的原因是_______________________.
(2)把正确的解题过程写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
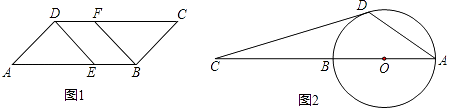
(1)如图1,在平行四边形ABCD中,已知点E在AB上,点F在CD上,且AE=CF.求证:DE=BF;
(2)如图2,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,求∠CDA的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系xOy(如图),直线 y=
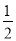 x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y=
x+b经过第一、二、三象限,与y轴交于点B,点A(2,t)在直线y= x+b上,连结AO,△AOB的面积等于1.
x+b上,连结AO,△AOB的面积等于1.(1)求b的值;
(2)如果反比例函数y=
 (k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.
(k是常量,k≠0)的图象经过点A,求这个反比例函数的表达式.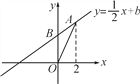
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)(2017·黄冈)已知:如图,一次函数y=-2x+1与反比例函数y=
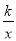 的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连结DE.
的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连结DE.(1)求k的值;
(2)求四边形AEDB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

