【题目】某公司计划从本地向甲、乙两地运送海产品共30吨进行销售.本地与甲、乙两地都有铁路和公路相连(如图所示),铁路的单位运价为2元/(吨千米),公路的单位运价为3元/(吨千米).
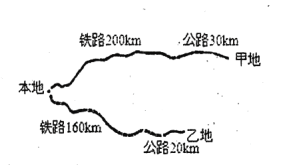
(1)公司计划从本地向甲地运输海产品![]() 吨,求总费用
吨,求总费用![]() (元)与
(元)与![]() 的函数关系式;
的函数关系式;
(2)公司要求运到甲地的海产品的重量不少于得到乙地的海产品重量的2倍,当![]() 为多少时,总运费
为多少时,总运费![]() 最低?最低总运费是多少元?(参考公式:货运运费
最低?最低总运费是多少元?(参考公式:货运运费![]() 单位运价
单位运价![]() 运输里程
运输里程![]() 货物重量)
货物重量)
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 为20时,总运费
为20时,总运费![]() 最低,最低总运费为13600元.
最低,最低总运费为13600元.
【解析】
(1)由公司计划从本地向甲地运输海产品x吨,可知公司从本地向乙地运输海产品(30x)吨,根据总运费=运往甲地海产品的运费+运往乙地海产品的运费,即可得出W关于x的函数关系式;
(2)由运到甲地的海产品的重量不少于运到乙地的海产品重量的2倍,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,再根据一次函数的性质即可解决最值问题.
解:(1)∵公司计划从本地向甲地运输海产品x吨,
∴公司从本地向乙地运输海产品(30x)吨.
根据题意得:W=200×2x+30×3x+160×2(30x)+20×3(30x)=110x+11400(0<x<30);
(2)根据题意得:x≥2(30x),
解得:x≥20.
在W=110x+11400中,110>0,
∴W值随x值的增大而增大,
∴当x=20时,W取最小值,最小值为13600.
答:当x为20时,总运费W最低,最低总运费是13600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:O是直线AB上的一点,
 是直角,OE平分
是直角,OE平分 .
.(1)如图1.若
 .求
.求 的度数;
的度数;(2)在图1中,
 ,直接写出
,直接写出 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);(3)将图1中的
 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究 和
和 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.
-
科目: 来源: 题型:
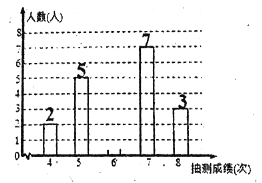
查看答案和解析>>【题目】为了解某校八年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成两个不完整的统计图,请结合图中信息回答下列问题:
(1)本次抽测的男生有 人,请将条形图补充完成,本次抽测成绩的中位数是 次;
(2)若规定引体向上6次及其以上为体能达标,则该校500名八年级男生中估计有多少人体能达标?

-
科目: 来源: 题型:
查看答案和解析>>【题目】松桃孟溪火车站一检修员某天乘一辆检修车在笔直的铁轨上来回检修,规定向东为正,从车站出发到收工时,行走记录为(单位:千米):+15,-2,-5,-1,+10,-3,-2,-12,+4,+6.
⑴计算收工时,检修员在车站的哪一边,此时,距车站多远?
⑵若汽车每千米耗油0.1升,且汽油的价格为每升6.8元,求这一天检修员从出发到收工时所耗油费是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了丰富学生的课余生活,宣传我县的旅游景点,某校将举行“我为松桃旅游代言”的活动,现随机抽取了部分学生进行主题为“你想去的景点是 ”的问卷调查,要求学生只能去“
 (正大苗王成),
(正大苗王成), (寨英古镇),
(寨英古镇), (盘石黔东草海),
(盘石黔东草海), (乌罗潜龙洞)”四个景点选择一项,根据调查结果,绘制了如下两幅不完整的统计图.回答下列问题:
(乌罗潜龙洞)”四个景点选择一项,根据调查结果,绘制了如下两幅不完整的统计图.回答下列问题:
⑴本次共调查了多少名学生;
⑵请把条形统计图补充完整;
⑶该学校共有3000名学生,试估计该校最想去盘石黔东草海的学生人数.
-
科目: 来源: 题型:
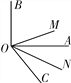
查看答案和解析>>【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
(1)如果∠AOC=50°,求∠MON的度数;
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?
相关试题

