【题目】阅读下列材料
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: ![]() .
.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: ![]() ,
, ![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: ![]() ,
, ![]() 这样的分式就是真分式.
这样的分式就是真分式.
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: ![]() ;
; ![]() ;
;
再如: ![]() .
.
解决下列问题:
(1)分式![]() 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式![]() 可化为带分式 的形式;
可化为带分式 的形式;
(3)如果分式![]() 的值为整数,那么x的整数值为 .
的值为整数,那么x的整数值为 .
参考答案:
【答案】(1)真;(2)![]() ;(3)0,-2,2,-4.
;(3)0,-2,2,-4.
【解析】试题分析:
(1)根据阅读材料中的内容可知:分式![]() 是真分式;
是真分式;
(2)参照阅读材料中的例子,把分式![]() 的分子化为
的分子化为![]() 即可把原分式化为带分式;
即可把原分式化为带分式;
(3)先把分式![]() 化成带分式的形式可得:
化成带分式的形式可得: ![]() ,由原分式的值为整数,可得
,由原分式的值为整数,可得![]() 的值为整数,由此即可分析得到整数
的值为整数,由此即可分析得到整数![]() 的值.
的值.
试题解析:
(1)由“真分式、假分式”的定义可知,分式![]() 是真分式;
是真分式;
(2)∵![]() ,
,
∴分式![]() 化为带分式的结果为:
化为带分式的结果为: ![]() ;
;
(3)∵![]() ,且
,且![]() 的值为整数,
的值为整数,
∴![]() 的值为整数,
的值为整数,
又∵![]() 的值为整数,
的值为整数,
∴![]() 或
或![]() ,
,
解得: ![]() 或
或![]() 或
或![]() 或
或![]() ,即
,即![]() 的整数值为
的整数值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校安排学生住宿,若每室住8人,则有12人无法安排;若每室住9人,可空出2个房间.这个学校的住宿生有_____人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】赵老师为了响应市政府“绿色出行”的号召,上下班由自驾车方式改为骑自行车方式.已知赵老师家距学校20千米,上下班高峰时段,自驾车的速度是自行车速度的2倍,骑自行车所用时间比自驾车所用时间多
 小时.求自驾车速度和自行车速度各是多少?
小时.求自驾车速度和自行车速度各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是( )
A. AB=CD,AD=BC,AC=BD B. AO=CO,BO=DO,∠A=90°
C. ∠A=∠C,∠B+∠C=180°,AC⊥BD D. ∠A=∠B=90°,AC=BD
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求画图,并回答问题.
已知:直线AB、CD相交于点O,且
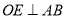
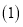 过点O画直线
过点O画直线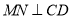 ;
; 若点F是
若点F是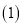 所画直线MN上任意一点
所画直线MN上任意一点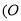 点除外
点除外 ,且
,且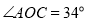 ,求
,求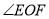 的度数.
的度数.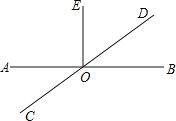
相关试题

