【题目】某公司计划投入50万元，开发并生产甲乙两种产品，根据市场调查预计甲产品的年获利y1（万元）与投入资金x（万元）成正比例，乙产品的年获利y2（万元）与投入资金x（万元）的平方成正比例，设该公司投入乙产品x（万元），两种产品的年总获利为y万元（x≥0），得到了表中的数据．
x（万元） | 20 | 30 |
y（万元） | 10 | 13 |
（1）求y与x的函数关系式；
（2）该公司至少可获得多少利润？请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议，使他能获得最大利润，并求出最大利润是多少？
（3）若从年总利润扣除投入乙产品资金的a倍（a≤1）后，剩余利润随x增大而减小，求a的取值
范围．
【答案】(1) 
;(2)见解析；(3) 0.8≤a≤1.
【解析】试题分析：（1）设y1=k1（50-x），y2= k2 x，则y= k1（50-x）+ k2 x，代入表格数据，求出k1，k2的值，即可得到结论；
（2）由题意求出x的范围，由二次函数的性质即可得到结论；
（3）求出
的表达式，利用二次函数的性质解答即可．
试题解析：解：（1）由题意可得：y1=k1（50-x），y2= k2 x，∴y= k1（50-x）+ k2 x，由表格可得：
，解得：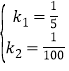
，
=
；
（2）由题意可知50≥x≥0．∵a=
＞0，∴当x=10时，y最小=9（万元），
当x=50时，y最大=25（万元），此时投入甲0万元，投入乙50万元．
（3）=
=
，对称轴为x=50a+10，
∵a=＞0，∴当x≤50a+10时，剩余利润随x增大而减小，又50≥x≥0，
∴当50≤50a+10，即a≥0.8时，剩余利润随x增大而减小，又a≤1，∴0.8≤a≤1．
阅读快车系列答案科目：初中数学 来源： 题型：
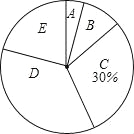
【题目】今年5月份，某校九年级学生参加了南宁市中考体育考试，为了了解该校九年级（1）班同学的中考体育情况，对全班学生的中考体育成绩进行了统计，并绘制以下不完整的频数分布表（如表）和扇形统计图（如图），根据图表中的信息解答下列问题：
（1）求全班学生人数和m的值．
（2）直接写出该班学生的中考体育成绩的中位数落在哪个分数段．
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率．
分组 | 分数段（分） | 频数 |
A | 36≤x＜41 | 2 |
B | 41≤x＜46 | 5 |
C | 46≤x＜51 | 15 |
D | 51≤x＜56 | m |
E | 56≤x＜61 | 10 |
查看答案和解析>>
科目：初中数学 来源： 题型：
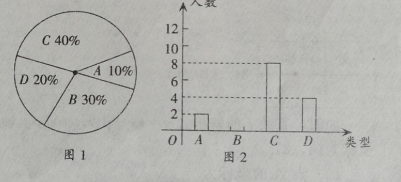
【题目】某校要求200名学生进行社会调查，每人必须完成3~6份报告，调查结束后随机抽查了20名学生每人完成报告的份数，并分为四类，A：3份；B：4份；C：5份；D：6份 各类的人数绘制成扇形图（如图1）和尚未完整的条形图（如图2），回答下列问题：
（1）请将条形统计图2补充完整；
（2）写出这20名学生每天完成报告份数的众数 份和中位数；
（3）在求出20名学生每人完成报告份数的平均数时，小明是这样分析的 第一步：求平均数的公式是
=
+
+
+…+
）
第二步：在该问题中，n=4 
=3， 
=4， 
=5 
=6
第三步
=
（3+4+5+6）=4.5（份）
小明的分析对不对？如果对，请说明理由，如果不对，请求出正确结果；
（4）现从“D类”的学生中随机选出2人进行采访，若“D类”的学生中只有1名 男生，则所选两位同学中有男同学的概率是多少？请用列表法或树状图的方法求解．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线l的解析式y=kx+3（k<0）与y轴交于A点，
与x轴交于点B．点C的坐标为（4，2）．
（1）点A的坐标为 ；
（2）若将△AOB沿直线l折叠，能否使点O与点C重合，若能求此时直线l的解析式；若不能，请说明理由。
（3）若点C在直线l的下方，求k的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
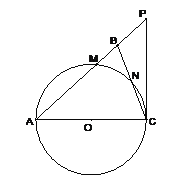
【题目】如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP.
（1）求证：直线CP是⊙O的切线；
（2）若BC=2
，sin∠BCP=
，求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点A(0，a)，B(b，12－b)，C(2a－3，0)，0＜a＜b＜12，若OB平分∠AOC，且AB＝BC，则a＋b的值为（ ）
A. 9或12B. 9或11C. 10或11D. 10或12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“十一”长假期间，小张和小李决定骑自行车外出旅游，两人相约一早从各自家中出发，已知两家相距10千米，小张出发必过小李家．
(1)若两人同时出发，小张车速为20千米，小李车速为15千米，经过多少小时能相遇？
(2)若小李的车速为10千米，小张提前20分钟出发，两人商定小李出发后半小时二人相遇，则小张的车速应为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一副直角三角尺的直角顶点C叠放在一起．
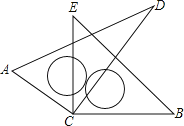
（1）若∠DCE＝35°，∠ACB＝ ；若∠ACB＝140°，则∠DCE＝ ；
（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；
（3）若保持三角尺BCE（其中∠B＝45°）不动，三角尺ACD的CD边与CB边重合，然后将三角尺ACD（其中∠D＝30°）绕点C按逆时针方向任意转动一个角度∠BCD．
设∠BCD＝α（0°＜α＜90°）
①∠ACB能否是∠DCE的4倍？若能求出α的值；若不能说明理由．
②当这两块三角尺各有一条边互相垂直时直接写出α的所有可能值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
