【题目】如图,一艘巡逻艇航行至海面B处时,得知正北方向上距B处20海里的C处有一渔船发生故障,就立即指挥港口A处的救援艇前往C处营救.已知C处位于A处的北偏东45°的方向上,港口A位于B的北偏西30°的方向上.求A、C之间的距离.(结果精确到0.1海里,参考数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)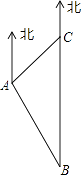
参考答案:
【答案】解:作AD⊥BC,垂足为D,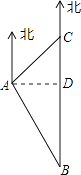
由题意得,∠ACD=45°,∠ABD=30°,
设CD=x,在Rt△ACD中,可得AD=x,
在Rt△ABD中,可得BD= ![]() x,
x,
又∵BC=20,即x+ ![]() x=20,
x=20,
解得: ![]()
∴AC= ![]() x≈10.3(海里).
x≈10.3(海里).
答:A、C之间的距离为10.3海里.
【解析】作AD⊥BC,垂足为D,设CD=x,利用解直角三角形的知识,可得出AD,继而可得出BD,结合题意BC=CD+BD=20海里可得出方程,解出x的值后即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCED的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )

A. 2∠A=∠1﹣∠2 B. 3∠A=2(∠1﹣∠2)
C. 3∠A=2∠1﹣∠2 D. ∠A=∠1﹣∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是 .(不再添加辅助线和字母)
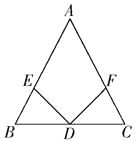
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一块a×b×c的长方体铁块(如图1所示,a<b<c,单位:cm)放入一长方体(如图2所示)水槽中,并以速度20cm3/s匀速向水槽注水,直至注满为止.若将铁块a×c面放至水槽的底面,则注水全过程中水槽的水深y (cm)与注水时间t (s)的函数图象如图3所示(水槽各面的厚度忽略不计).已知a为5cm.
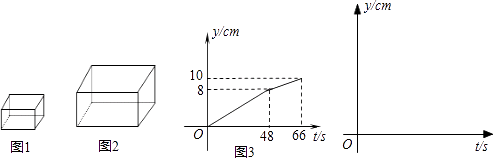
(1)填空:水槽的深度为cm,b=cm;
(2)求水槽的底面积S和c的值;
(3)若将铁块的b×c面放至水槽的底面,求注水全过程中水槽的水深y(cm)与注水时间t(s)的函数关系,写出t的取值范围,并画出图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元? 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 ,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
,经过A、B的直线l以每秒1个单位的速度向下作匀速平移运动,与此同时,点P从点B出发,在直线l上以每秒1个单位的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
(1)用含t的代数式表示点P的坐标;
(2)过O作OC⊥AB于C,过C作CD⊥x轴于D,问:t为何值时,以P为圆心、1为半径的圆与直线OC相切?并说明此时⊙P与直线CD的位置关系.
相关试题

