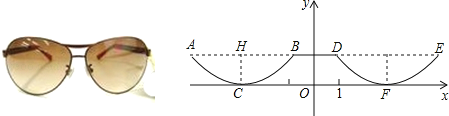
【题目】如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=![]() (x+3)2
(x+3)2
B.y=![]() (x+3)2
(x+3)2
C.y=![]() (x﹣3)2
(x﹣3)2
D.y=![]() (x﹣3)2
(x﹣3)2
参考答案:
【答案】C
【解析】
试题分析:利用B、D关于y轴对称,CH=1cm,BD=2cm可得到D点坐标为(1,1),由AB=4cm,最低点C在x轴上,则AB关于直线CH对称,可得到左边抛物线的顶点C的坐标为(﹣3,0),于是得到右边抛物线的顶点C的坐标为(3,0),然后设顶点式利用待定系数法求抛物线的解析式.
解:∵高CH=1cm,BD=2cm,
而B、D关于y轴对称,
∴D点坐标为(1,1),
∵AB∥x轴,AB=4cm,最低点C在x轴上,
∴AB关于直线CH对称,
∴左边抛物线的顶点C的坐标为(﹣3,0),
∴右边抛物线的顶点C的坐标为(3,0),
设右边抛物线的解析式为y=a(x﹣3)2,
把D(1,1)代入得1=a×(1﹣3)2,解得a=![]() ,
,
故右边抛物线的解析式为y=![]() (x﹣3)2.
(x﹣3)2.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出“线段垂直平分线上的点到线段两端距离相等”的逆命题____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
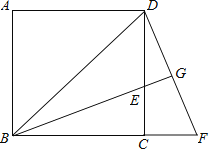
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解全校七年级300名学生的视力情况,骆老师从中抽查了50名学生的视力情况.针对这个问题,下面说法正确的是( )
A. 300名学生是总体 B. 每名学生是个体
C. 50名学生是所抽取的一个样本 D. 这个样本容量是50
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(-3,4)位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣1,4)向右平移2个单位后,再向上平移1个单位,得A1,则A1点的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3(x﹣2)2=27
(2)2(x﹣1)3+16=0.
相关试题

