【题目】如图在平面直角坐标系xOy中,函数y= ![]() (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).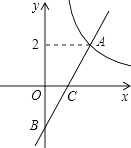
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
参考答案:
【答案】
(1)解:将A(m,2)代入y= ![]() (x>0)得,
(x>0)得,
m=2,
则A点坐标为A(2,2),
将A(2,2)代入y=kx﹣k得,2k﹣k=2,
解得k=2,则一次函数解析式为y=2x﹣2
(2)解:∵一次函数y=2x﹣2与x轴的交点为C(1,0),与y轴的交点为B(0,﹣2),

S△ABP=S△ACP+S△BPC,
∴ ![]() ×2CP+
×2CP+ ![]() ×2CP=4,
×2CP=4,
解得CP=2,
则P点坐标为(3,0),(﹣1,0).
【解析】(1)将点A的坐标代入反比例函数解析式,即可求出点A的坐标,再用待定系数法求出一次函数的解析式。
(2)点P的位置关系有两种:点P在点C的左侧和右侧,观察图像易得S△ABP=S△ACP+S△BPC=4,求出CP的长,就可以求出点P的坐标。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民低碳生活绿色出行,市政府计划改造如图所示的人行天桥:天桥的高是10米,原坡面倾斜角∠CAB=45°.
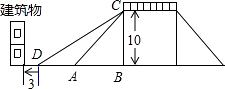
(1)若新坡面倾斜角∠CDB=28°,则新坡面的长CD长是多少?(精确到0.1米)
(2)若新坡角顶点D前留3米的人行道,要使离原坡角顶点A处10米的建筑物不拆除,新坡面的倾斜角∠CDB度数的最小值是多少?(精确到1°) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校“体育课外活动兴趣小组”,开设了以下体育课外活动项目:A.足球 B.乒乓球C.羽毛球 D.篮球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
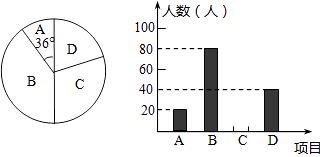
(1)这次被调查的学生共有人,在扇形统计图中“D”对应的圆心角的度数为;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加市里组织的乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答). -
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y+z=15,-3x-y+z=-25,x、y、z皆为非负数,记整式5x+4y+z的最大值为a,最小值为b,则a﹣b =________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂设门市部专卖某产品,该每件成本每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元)
50
60
70
75
80
85
…
日销售量
300
240
180
150
120
90
…
假设每天定的销价是不变的,且每天销售情况均服从这种规律.
(1)秋日销售量与销售价格之间满足的函数关系式;
(2)门市部原设定两名销售员,担当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步了解七年级800名学生的身体素质情况,体育老师抽取七年级男女各25位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140

第4组
140≤x<160
16
第5组
160≤x<180
6

请结合图表完成下列问题:
(1)表中的
 ,跳绳次数低于140次的有
,跳绳次数低于140次的有 人,则
人,则
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:x≥120.请估算七年级学生达标人数.
相关试题

