搜索
【题目】如图⊙O是△ABC的外接圆，圆心O在这个三角形的高AD上，AB=10，BC=12，求⊙O的半径．
参考答案：
【答案】解：如图，连接OB．
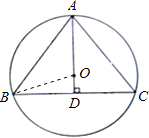
∵AD是△ABC的高．
∴BD= 
BC=6
在Rt△ABD中，AD= 
= 
=8．
设圆的半径是R．
则OD=8﹣R．
在Rt△OBD中，根据勾股定理可以得到：R2=36+（8﹣R）2
解得：R= 
．
【解析】连接OB，根据垂经定理求出BD的长，在Rt△ABD中由勾股定理求得AD=8，设圆的半径是R，则OD=8-R，在Rt△OBD中由勾股定理可求得R的值.解答此题的关键是作出辅助线OB.注意：垂径定理和勾股定理常常在一起中应用.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知E，F分别是AB、CD上的动点，P也为一动点．
（1）如图1，若AB∥CD，求证：∠P＝∠BEP＋∠PFD；
（2）如图2，若∠P＝∠PFD－∠BEP，求证：AB∥CD；
（3）如图3，AB∥CD，移动E，F使得∠EPF＝90°，作∠PEG＝∠BEP，求
的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探索研究：已知：△ABC和△CDE都是等边三角形．
（1）如图1，若点A、C、E在一条直线上时，我们可以得到结论：线段AD与BE的数量关系为： ，线段AD与BE所成的锐角度数为 °；
（2）如图2，当点A、C、E不在一条直线上时，请证明（1）中的结论仍然成立；
灵活运用：
如图3，某广场是一个四边形区域ABCD，现测得：AB＝60m，BC＝80m，且∠ABC＝30°，∠DAC＝∠DCA＝60°，试求水池两旁B、D两点之间的距离．
-
科目： 来源： 题型：
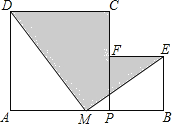
查看答案和解析>>【题目】如图，点M是AB的中点，点P在MB上．分别以AP，PB为边，作正方形APCD和正方形PBEF，连结MD和ME．设AP＝a，BP＝b，且a+b＝10，ab＝20．则图中阴影部分的面积为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小刚同学动手剪了如图①所示的正方形与长方形纸片若干张．
（1）他用1张1号、1张2号和2张3号卡片拼出一个新的图形（如图②）．根据这个图形的面积关系写出一个你所熟悉的乘法公式，这个乘法公式是 ；
（2）如果要拼成一个长为（a+2b），宽为（a+b）的大长方形，则需要2号卡片 张，3号卡片 张；
（3）当他拼成如图③所示的长方形，根据6张小纸片的面积和等于打纸片（长方形）的面积可以把多项式a2+3ab+2b2分解因式，其结果是 ；
（4）动手操作，请你依照小刚的方法，利用拼图分解因式a2+5ab+6b2= 画出拼图．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店甲、乙两种商品三天销售情况的账目记录如下表：
日期
卖出甲商品的数量(个)
卖出乙商品的数量(个)
收入(元)
第一天
39
21
321
第二天
26
14
204
第三天
39
25
345
(1)财务主管在核查时发现：第一天的账目正确，但其他两天的账目有一天有误，请你判断第几天的账目有误，并说明理由；
(2)求甲、乙两种商品的单价．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一矩形OABC放在直角坐标系中，O为坐标原点，点A在y轴正半轴上，点E是边AB上的一个动点（不与点A、B重合），过点E的反比例函数y=
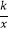（x＞0）的图象与边BC交与点F．
（1）若△OAE、△OCF的面积分别为S1、S2 ， 且S1+S2=2，求k的值；
（2）在（1）的结论下，当OA=2，OC=4时，求三角形OEF的面积．
相关试题
