【题目】如图1,点P、Q分别是边长为4cm的等边三角形ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.

(1)连接AQ、CP交于点M,则在P,Q运动的过程中,证明![]() ≌
≌![]() ;
;
(2)![]() 会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
会发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
(3)P、Q运动几秒时,![]() 是直角三角形?
是直角三角形?
(4)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则![]() 变化吗?若变化说明理由,若不变,则求出它的度数。
变化吗?若变化说明理由,若不变,则求出它的度数。
参考答案:
【答案】(1)见解析;(2)∠CMQ=60°,不变;(3)当第![]() 秒或第2秒时,△PBQ为直角三角形;(4)∠CMQ=120°,不变.
秒或第2秒时,△PBQ为直角三角形;(4)∠CMQ=120°,不变.
【解析】
(1)利用SAS可证全等;
(2)先证△ABQ≌△CAP,得出∠BAQ=∠ACP,通过角度转化,可得出∠CMQ=60°;
(3)存在2种情况,一种是∠PQB=90°,另一种是∠BPQ=90°,分别根据直角三角形边直角的关系可求得t的值;
(4)先证△PBC≌△ACQ,从而得出∠BPC=∠MQC,然后利用角度转化可得出∠CMQ=120°.
(1)证明:在等边三角形ABC中,AB=AC,∠B=∠CAP=60°
又由题中“点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.”可知:
AP=BQ
∴![]() ≌
≌![]() ;
;
(2)∠CMQ=60°不变
∵等边三角形中,AB=AC,∠B=∠CAP=60°
又由条件得AP=BQ,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;
(3)设时间为t,则AP=BQ=t,PB=4-t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得4-t=2t,t=![]() ;
;
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2PQ,得2t=2(4-t),t=2;
∴当第![]() 秒或第2秒时,△PBQ为直角三角形;
秒或第2秒时,△PBQ为直角三角形;
(4)∠CMQ=120°不变,
∵在等边三角形中,AB=AC,∠B=∠CAP=60°,
∴∠PBC=∠ACQ=120°,
又由条件得BP=CQ,
∴△PBC≌△ACQ(SAS),
∴∠BPC=∠MQC,
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=180°-60°=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程
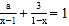 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?经过小组交流讨论后,同学们逐渐形成了两种意见:
小明说:解这个关于x的分式方程,得到方程的解为x=a﹣2.由题意可得a﹣2>0,所以a>2,问题解决.
小强说:你考虑的不全面.还必须保证a≠3才行.
老师说:小强所说完全正确.
请回答:小明考虑问题不全面,主要体现在哪里?请你简要说明: .
完成下列问题:
(1)已知关于x的方程
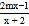 =1的解为负数,求m的取值范围;
=1的解为负数,求m的取值范围;(2)若关于x的分式方程
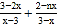 =﹣1无解.直接写出n的取值范围.
=﹣1无解.直接写出n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(4,2)、B(a,4)是一次函数y=kx+b的图象与反比例函数
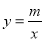 的图象的两个交点;
的图象的两个交点;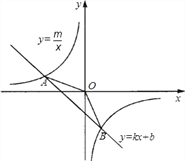
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
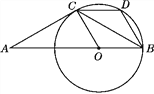
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克)
…
50
60
70
80
…
销售量y(千克)
…
100
90
80
70
…
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶
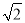 B. 1∶2 C.
B. 1∶2 C. 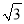 ∶2 D. 1∶
∶2 D. 1∶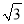
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2x+k=0.
(1)若方程有实数根,求k的取值范围;
(2)如果k是满足条件的最大的整数,且方程x2-2x+k=0一根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一根.
相关试题

