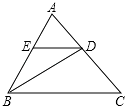
【题目】把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
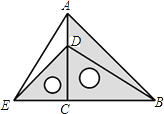
【答案】BF⊥AE,理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD,CA=CB,∠ACE=∠BCD=90°,∴△BCD≌△ACE,∴BD=AE,∠CBD=∠CAE,∵∠CAE+∠AEC=90°,∴∠CBD+∠AEC=90°,∴∠BFE=90°,即BD⊥AE.
【题型】解答题
【结束】
24
【题目】在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
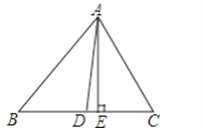
参考答案:
【答案】∠DAE=5°.
【解析】试题分析:根据三角形内角和定理求出∠BAC的度数,再根据角平分线的定义求得∠CAD的度数;在△AEC中,求出∠CAE的度数,从而可得∠DAE的度数.
试题解析:
∵在△ABC中,∠B=50°,∠C=60°,
∴∠BAC=180°﹣50°﹣60°=70°.
∵AD平分∠BAC,
∴∠CAD=![]() ∠BAC=35°.
∠BAC=35°.
∵AE⊥BC于E,
∴∠CAE=90°﹣60°=30°,
∴∠DAE=∠CAD﹣∠CAE=35°﹣30°=5°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
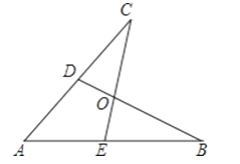
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中,
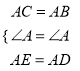 ,
,∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中,
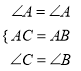 ,
,∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中,
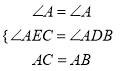 ,
,∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点睛:本题考查了全等三角形的判定方法,是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.
【题型】填空题
【结束】
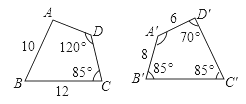
17【题目】如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________,∠A=________,B′C′=________,AD=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )

A.4.5
B.5
C.5.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=20cm,AC=12cm,点P从点B出发以每秒3cm速度向点A运动,点Q从点A同时出发以每秒2cm速度向点C运动,其中一个动点到达端点,另一个动点也随之停止,当△APQ是以PQ为底的等腰三角形时,运动的时间是秒.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.
相关试题

