【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
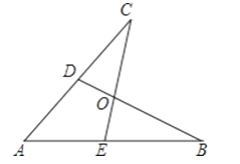
【答案】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC
【解析】AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC;理由如下:
若AD=AE,
在△ACE和△ABD中, 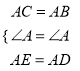 ,
,
∴△ACE≌△ABD(SAS);
若CD=BE,
∵AB=AC,
∴AD=AE,
同理:△ACE≌△ABD(SAS);
若∠B=∠C,
在△ACE和△ABD中, 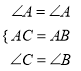 ,
,
∴△ACE≌△ABD(ASA);
若∠ADB=∠AEC,
在△ACE和△ABD中, 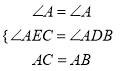 ,
,
∴△ACE≌△ABD(AAS);
故答案为:AD=AE或CD=BE或∠B=∠C或∠ADB=∠AEC.
点睛:本题考查了全等三角形的判定方法,是开放型题目,存在四种情况,熟练掌握全等三角形的判定方法是解决问题的关键.
【题型】填空题
【结束】
17
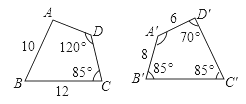
【题目】如图,四边形ABCD与四边形A′B′C′D′全等,则∠A′=________,∠A=________,B′C′=________,AD=________.
参考答案:
【答案】120°;70°;12;6
【解析】∵四边形ABCD与四边形A′B′C′D′全等,
由题意得:∠A′=∠D =∠120°,∠D′=∠A=70°,B′C′=CB=12,AD = D′A′=6.
-
科目: 来源: 题型:
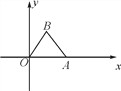
查看答案和解析>>【题目】如图,△OAB的OA边在x轴上,其中B点坐标为(3,4)且OB=BA.
(1)求经过A,B,O三点的抛物线的解析式;
(2)将(1)中的抛物线沿x轴平移,设点A,B的对应点分别为点A′,B′,若四边形ABB′A′为菱形,求平移后的抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )
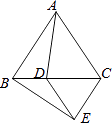
A.∠BDE=120°
B.∠ACE=120°
C.AB=BE
D.AD=BE -
科目: 来源: 题型:
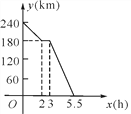
查看答案和解析>>【题目】端午节假时,李明一家人驾车从宝鸡到汉中游玩,下图是他们距离汉中的路程y(km)与路上耗时x(h)之间的函数关系图象.
(1)请你根据图象写出路程y(km)与路上耗时x(h)之间的函数关系式;
(2)他们出发3.5 h时共行驶了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )

A.4.5
B.5
C.5.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=54°,∠C=66°,求∠DAC、∠BOA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
【答案】BF⊥AE,理由详见解析.
【解析】BD=AE ,BD⊥AE.延长BD交AE于F ,证△BCD≌△ACE,可得BD=AE ,BD⊥AE .
∵CE=CD,CA=CB,∠ACE=∠BCD=90°,∴△BCD≌△ACE,∴BD=AE,∠CBD=∠CAE,∵∠CAE+∠AEC=90°,∴∠CBD+∠AEC=90°,∴∠BFE=90°,即BD⊥AE.
【题型】解答题
【结束】
24【题目】在△ABC中,已知∠B=50°,∠C=60°,AE⊥BC于E,AD平分∠BAC;求:∠DAE的度数.
相关试题

