【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数![]() (x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
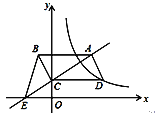
A. 2 B. ﹣2 C. 3 D. 4
参考答案:
【答案】D
【解析】连接ED、OD,由平行四边形的性质可得出BC=AD,AD⊥AC,根据同底等高的三角形面积相等即可得出S△BCE=S△DCE,同理得出S△OCD=S△DCE,再利用反比例函数系数K几何意义即可求出结论.
解:连接ED、OD,如图所示,
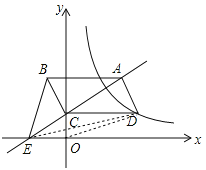
∵四边形ABCD为平行四边形,
∴BC=AD,BC∥AD,
∵BC⊥AC,
∴AD⊥AC,
∵S△BCE和S△DCE有相同的底CE,相等的高BC=AD,
∴S△OCD=S△DCE,
∵CD平行于x轴,
∴△OCD与△ECD有相等的高,
∴S△OCD=S△DCE=S△BCE=2=![]() ,
,
∴![]() ,
,
∵反比例函数在第一象限有图象,
∴![]() ,
,
故选:D.
“点睛”本题考查了反比例函数系数K何意义、平行四边形的性质以及平行线的性质,利用同底等高的三角形面积相等找出S△OCD=S△DCE=S△BCE是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“因为a//b,b//c,所以a//c” ,这个推理的依据是( )
A. 过直线外一点,有且只有一条直线与已知直线垂直
B. 垂线段最短
C. 平行于同一直线的两条直线平行
D. 过一点有且只有一条直线与已知直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算3﹣(﹣1)的结果是( )
A.﹣4
B.﹣2
C.2
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
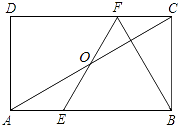
(1)求证:OE=OF;
(2)若BC=2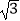 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1的小正方形组成的方格纸中,若多边形的每个顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形.记格点多边形内的格点数为
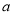 ,边界上的格点数为
,边界上的格点数为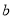 ,则格点多边形的面积可表示为
,则格点多边形的面积可表示为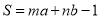 ,其中
,其中 ,
, 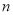 为常数.
为常数.(1)在下面的两张方格纸中各有一个格点多边形,依次为
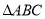 、正方形
、正方形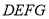 .认真数一数:
.认真数一数: 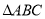 内的格点数是_______,正方形
内的格点数是_______,正方形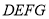 边界上的格点数是_______;
边界上的格点数是_______;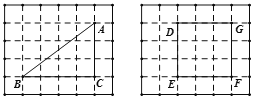
(2)利用(1)中的两个格点多边形确定
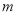 ,
, 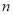 的值;
的值;(3)现有一张方格纸共有110个格点,画有一个格点多边形,它的面积
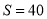 ,若该格点多边形外的格点数为
,若该格点多边形外的格点数为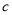 .
.①填空:若
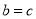 ,则
,则 = ;
= ;②若
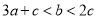 ,求
,求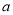 的值.(写出解答过程)
的值.(写出解答过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个外角都是60°,则这个多边形边数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒
 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?

相关试题

