【题目】在边长为1的小正方形组成的方格纸中,若多边形的每个顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形.记格点多边形内的格点数为![]() ,边界上的格点数为
,边界上的格点数为![]() ,则格点多边形的面积可表示为
,则格点多边形的面积可表示为![]() ,其中
,其中![]() ,
, ![]() 为常数.
为常数.
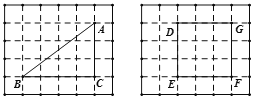
(1)在下面的两张方格纸中各有一个格点多边形,依次为![]() 、正方形
、正方形![]() .认真数一数:
.认真数一数: ![]() 内的格点数是_______,正方形
内的格点数是_______,正方形![]() 边界上的格点数是_______;
边界上的格点数是_______;
(2)利用(1)中的两个格点多边形确定![]() ,
, ![]() 的值;
的值;
(3)现有一张方格纸共有110个格点,画有一个格点多边形,它的面积![]() ,若该格点多边形外的格点数为
,若该格点多边形外的格点数为![]() .
.
①填空:若![]() ,则
,则![]() = ;
= ;
②若![]() ,求
,求![]() 的值.(写出解答过程)
的值.(写出解答过程)
参考答案:
【答案】(1)3,12;(2)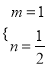 ;(3)①18;②
;(3)①18;②![]() =7或8
=7或8
【解析】试题分析:(1)利用格点图形的定义结合三角形以及正方形图形得出即可;
(2)利用已知图形,结合S=ma+nb-1得出关于m,n的关系式,进而求出即可;
(3)①由(2)知: ![]() ,将S=40代入和a+b+c=110联立消去b即可求得a的值;②由
,将S=40代入和a+b+c=110联立消去b即可求得a的值;②由![]() ,用a 表示出b,由
,用a 表示出b,由![]() 用a表示出c,带入
用a表示出c,带入![]() ,即可解得a的范围,由于a为整数,再确定出a的值即可.
,即可解得a的范围,由于a为整数,再确定出a的值即可.
试题解析:(1)由图可得: ![]() 内的格点数是3,正方形DEFG边界上的格点数是12;
内的格点数是3,正方形DEFG边界上的格点数是12;
(2):![]() 面积为
面积为![]() ×3×4=6,正方形DEFG面积为3×3=9,
×3×4=6,正方形DEFG面积为3×3=9,
依题意,得![]() ,解得
,解得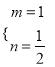 ;
;
(3)①∵a是多边形内的格点数,b是多边形边界上的格点数,c是多边形外的格点数,总格点数为110,
∴a+b+c=110,
∵![]() ,
,
∴a+2b =110,
由(2)知![]() ,
,
∴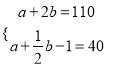 ,解得a=18.
,解得a=18.
故答案为:18;
②依题意,得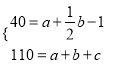 解得
解得![]()
代入![]() ,得
,得![]()
解不等式组,得![]()
∴整数![]() =7或8.
=7或8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算3﹣(﹣1)的结果是( )
A.﹣4
B.﹣2
C.2
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
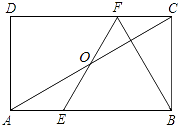
(1)求证:OE=OF;
(2)若BC=2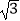 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数
 (x>0)的图象经过点D.已知S△BCE=1,则k的值是( )
(x>0)的图象经过点D.已知S△BCE=1,则k的值是( )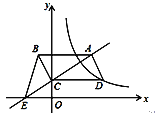
A. 2 B. ﹣2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每个外角都是60°,则这个多边形边数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒
 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?

-
科目: 来源: 题型:
查看答案和解析>>【题目】共享单车近日成为市民新宠,越来越多的居民选择共享单车作为出行的交通工具,某中学课外兴趣小组为了了解某小区居民每周使用共享单车时间的情况,随机抽取了该小区部分使用共享单车的居民进行调查(问卷调查表如图所示),并用调查结果绘制了图①、图②两幅每周使用共享单车时间的人数统计图(均不完整),请根据统计图解答以下问题:
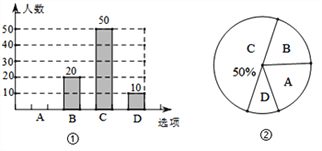
(1)本次接受问卷调查的共有 人;在扇形统计图中“D”选项所占的百分比为 ;
(2)扇形统计图中,“B”选项所对应扇形圆心角为 度;
(3)请补全条形统计图;
(4)若该小区共有1200名居民,请你估计该小区使用共享单车的时间在“A”选项的有多少人?
相关试题

