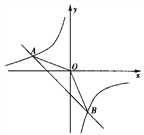
【题目】如图,一次函数![]() 的图象与反比例
的图象与反比例![]() 的图象相交于A(-2,1),B(
的图象相交于A(-2,1),B(![]() ,-2)两点.
,-2)两点.
(1)求反比例函数和一次函数的解析式;
(2) 求△ABO的面积.
参考答案:
【答案】(1)![]() ;(2)1.5.
;(2)1.5.
【解析】分析:(1)把A(﹣2,1)代入求出反比例函数的解析式,代入求出A的坐标,把A、B的坐标代入得到方程组,求出方程组的解即可;
(2)求出直线AB与x轴的交点C的坐标,根据三角形的面积公式求出即可.
详解:(1)把A(﹣2,1)代入反比例函数y=![]() 得:m=﹣2×1=﹣2,∴反比例函数为y=﹣
得:m=﹣2×1=﹣2,∴反比例函数为y=﹣![]() .
.
∵点(n,-2)在反比例函数上,∴n=1,∴B(1,﹣2),把A(﹣2,1),B(1,﹣2)代入得: ![]() ,解得:k=﹣1,b=﹣1,∴一次函数的解析式为y=﹣x﹣1.
,解得:k=﹣1,b=﹣1,∴一次函数的解析式为y=﹣x﹣1.
(2)设直线AB和x轴的交点为C,令y=0,则0=﹣x﹣1,∴x=﹣1,∴C(﹣1,0),∴OC=1,∴S△AOB=S△AOC+S△BOC=![]() ×1×1+
×1×1+![]() ×1×2=1.5.
×1×2=1.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店从厂家以21元的价格购进一批商品,该商品可以自行定价,若每件商品售价为
 元,则可卖出(350-10
元,则可卖出(350-10 )件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元?
)件,但物价局限定每件商品加价不能超过进价的20%,商店计划要赚400元,需要卖出多少件商品?每件商品应售多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师给出了如下问题:

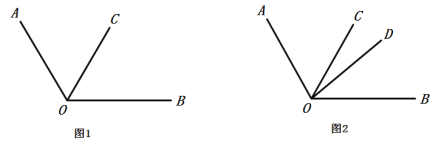
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为
 ,
,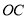 平分
平分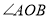 ,
,所以
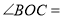 ______
______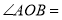 ______
______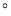 (角平分线的定义).
(角平分线的定义).因为
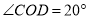 ,
,所以
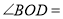 ______
______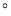 .
.(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是
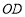 在
在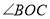 内部的情况,事实上,
内部的情况,事实上,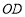 还可能在
还可能在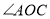 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出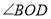 的度数:______.
的度数:______. -
科目: 来源: 题型:
查看答案和解析>>【题目】某人将10000元存入银行,一年后取出5000元,再将余下的本利和再存入银行,但此时银行的年利率已下降3个百分点,且到期后还要缴20%的利息税·第二年到期他取出全部存款共5588元,求银行原来的年利率.
-
科目: 来源: 题型:
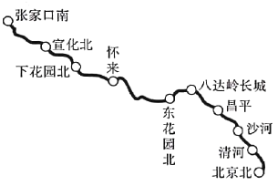
查看答案和解析>>【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数轴上的
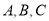 三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两点的“倍联点”. 例如数轴上点
三点,给出如下定义:若其中一个点与其他两个点的距离恰好满足2倍的数量关系,则称该点是其他两点的“倍联点”. 例如数轴上点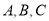 所表示的数分别为1,3,4,满足
所表示的数分别为1,3,4,满足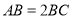 ,此时点
,此时点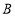 是点
是点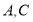 的“倍联点”.
的“倍联点”. 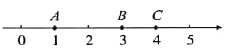
若数轴上点
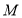 表示
表示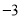 ,点
,点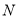 表示6,回答下列问题:
表示6,回答下列问题:(1)数轴上点
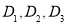 分別对应0,3. 5和11,则点_________是点
分別对应0,3. 5和11,则点_________是点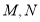 的“倍联点”,点
的“倍联点”,点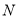 是________这两点的“倍联点”;
是________这两点的“倍联点”;(2)已知动点
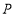 在点
在点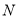 的右侧,若点
的右侧,若点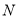 是点
是点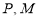 的倍联点,求此时点
的倍联点,求此时点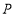 表示的数.
表示的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】李老伯想用24米长的旧木料,靠
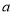 米长的围墙造一个如图所示的猪舍,它们的平面图是一排大小相等的三个长方形,总面积为32平方米.
米长的围墙造一个如图所示的猪舍,它们的平面图是一排大小相等的三个长方形,总面积为32平方米.(1)求猪舍的长BC和宽AB各为多少米?
(2)题中围墙的长度
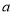 米对猪舍的长和宽是否有影响?怎样影响?
米对猪舍的长和宽是否有影响?怎样影响?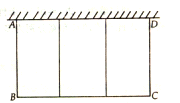
相关试题

