【题目】阅读下列材料:
一般地,n个相同的因数a相乘![]() 记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
记为an,记为an.如2×2×2=23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
(1)计算以下各对数的值:
log24= ,log216= ,log264= .
(2)观察(1)中三数4、16、64之间满足怎样的关系式,log24、log216、log264之间又满足怎样的关系式 。
(3)由(2)的结果,你能归纳出一个一般性的结论吗?
logaM+logaN= ;(a>0且a≠1,M>0,N>0)
(4)根据幂的运算法则:anam=an+m以及对数的含义证明上述结论.
参考答案:
【答案】(1)2,4,6;(2)4×16=64,log24+log216=log264;(3)loga(MN);(4)证明见解析.
【解析】试题分析:首先认真阅读题目,准确理解对数的定义,把握好对数与指数的关系.
(1)根据对数的定义求解;
(2)认真观察,不难找到规律:4×16=64,log24+log216=log264;
(3)有特殊到一般,得出结论:logaM+logaN=loga(MN);
(4)首先可设logaM=b1,logaN=b2,再根据幂的运算法则:anam=an+m以及对数的含义证明结论.
试题解析:(1)log24=2,log216=4,log264=6;
(2)4×16=64,log24+log216=log264;
(3)logaM+logaN=loga(MN);
(4)证明:设logaM=b1,logaN=b2,
则ab1=M,ab2=N,
∴MN=ab1ab2=ab1+b2,
∴b1+b2=loga(MN)即logaM+logaN=loga(MN).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,  平分
平分 ,
,  于点
于点 .
.(1)求
 的度数.
的度数.(2)求证:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
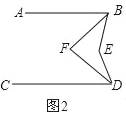
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列各式中的x的值:
(1)8x3+125=0;
(2)(x-3)2-9=0.
【答案】(1)x=-
 ;(2)x1=6或x2=0.
;(2)x1=6或x2=0.【解析】试题分析:(1)立方根定义解方程.(2)平方根定义解方程.
试题解析:(1)8x3+125=0,
x3=
 ,
,x=-
 .
.(2)(x-3)2-9=0,
(x-3)2=9,
x-3=
 ,
,x1=6或x2=0.
【题型】解答题
【结束】
19【题目】(1)已知某数的平方根是
 和
和 ,
,  的立方根是
的立方根是 ,求
,求 的平方根.
的平方根.(2)已知y=
 +
+ -8,求
-8,求 的值.
的值. -
科目: 来源: 题型:
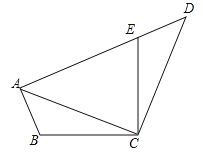
查看答案和解析>>【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析:
 根据同角的余角相等可得到
根据同角的余角相等可得到 结合条件
结合条件 ,再加上
,再加上 可证得结论;
可证得结论; 根据
根据 得到
得到 根据等腰三角形的性质得到
根据等腰三角形的性质得到 由平角的定义得到
由平角的定义得到
试题解析:
 证明:
证明: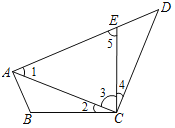



在△ABC和△DEC中,
 ,
,

(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】向阳中学数学兴趣小组对关于x的方程(m+1)
 +(m﹣2)x﹣1=0提出了下列问题:
+(m﹣2)x﹣1=0提出了下列问题:(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
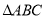 中,
中, 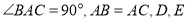 是
是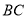 边上的点,将
边上的点,将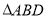 绕点
绕点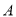 旋转,得到
旋转,得到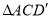 .
.(1)当
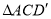 时,求证:
时,求证: 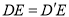 .
.(2)在(1)的条件下,猜想
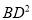 ,
, 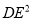 ,
, 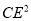 有怎样的数量关系,并说明理由.
有怎样的数量关系,并说明理由.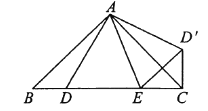
相关试题

