【题目】在△ABC中,AB=15,AC=13,高AD=12,则BC的长是____.
参考答案:
【答案】14或4
【解析】试题分析:分两种情况讨论:锐角三角形和钝角三角形,根据勾股定理求得BD,CD,再由图形求出BC,在锐角三角形中,BC=BD+CD,在钝角三角形中,BC=CD-BD.
试题解析:(1)如图,
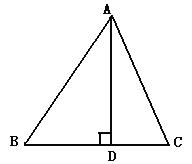
锐角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2-AD2=152-122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得
CD2=AC2-AD2=132-122=25,
∴CD=5,
∴BC的长为BD+DC=9+5=14;
(2)如图:
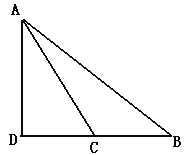
钝角△ABC中,AB=15,AC=13,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,由勾股定理得:
BD2=AB2-AD2=152-122=81,
∴BD=9,
在Rt△ACD中AC=13,AD=12,由勾股定理得:
CD2=AC2-AD2=132-122=25,
∴CD=5,
∴BC的长为DC-BD=9-5=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列所给出的坐标中,在第二象限的是( )
A. (2,3) B. (2,-3) C. (-2,-3) D. (-2,3)
-
科目: 来源: 题型:
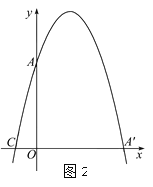
查看答案和解析>>【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(1,2)关于原点O对称的点P′的坐标为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆锥底面圆的半径为1,侧面积等于3π,则它的母线长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请把命题“对顶角相等。”写成“如果……,那么……。”的形式:_______________
相关试题

