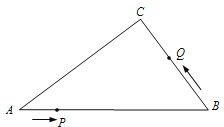
【题目】如图,在Rt△ABC中,∠C=90,AB=10cm,AC∶BC=4∶3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
(1)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(2)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由.
(3)当点Q在BC边上运动时,是否存在x,使得以△PBQ的一个顶点为圆心作圆时,另外两个顶点均在这个圆上,若存在,求出 x的值;不存在,说明理由.
参考答案:
【答案】(1)、y=-![]() +8x(0<x≤3),y=
+8x(0<x≤3),y=![]() ;(2)、16;(3)、x=
;(2)、16;(3)、x=![]() .
.
【解析】
试题分析:(1)、分点Q在边BC上和点Q在边CA上运动;(2)、根据AQ=14﹣2x=14﹣10=4,AP=x=5以及AC=8,AB=10,从而得出PQ是AC的垂直平分线,则PC=AP=5,即当点M与P重合时,△BCM的周长最小;(3)、本题需要分三种情况得出答案.
试题解析:(1)、①当点Q在边BC上运动时.y=-![]() +8x(0<x≤3),
+8x(0<x≤3),
②当点Q在边CA上运动时,y=![]() =
=![]() (3<x<7);
(3<x<7);

(2)、存在. 理由:∵AQ=14﹣2x=14﹣10=4,AP=x=5, ∵AC=8,AB=10,
∴PQ是△ABC的中位线, ∴PQ∥AB,∴PQ⊥AC, ∴PQ是AC的垂直平分线,
∴PC=AP=5, ∴当点M与P重合时,△BCM的周长最小,
∴△BCM的周长为: MB+BC+MC=PB+BC+PC=5+6+5=16. ∴△BCM的周长最小值为16.
(3)、由题意得△PBQ为等腰三角形。
①PQ=PB,x=![]() >3(舍) ②BQ=BP,x=
>3(舍) ②BQ=BP,x=![]() >3(舍) ③QP=QB,x=
>3(舍) ③QP=QB,x=![]() ,
,
综上所述,存在满足题意得x,x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x、y的方程组
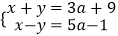 的解是一对正数,求a的取值范围.
的解是一对正数,求a的取值范围. -
科目: 来源: 题型:
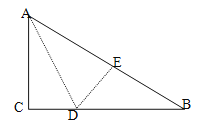
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式组
 ,的整数解是关于x的方程2x-4=ax的根,求a的值.
,的整数解是关于x的方程2x-4=ax的根,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】多项式 3a2﹣2a﹣7a3+4 是________次四项式,最高次项是______,常数项是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=(x﹣2)2+1化为y=x2+bx+c的形式,其中b、c为常数,则b+c= .
相关试题

