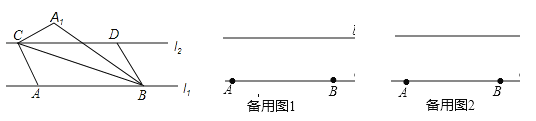
【题目】已知:直线l1与直线l2平行,且它们之间的距离为2,A、B是直线l1上的两个定点,C、D是直线l2上的两个动点(点C在点D的左侧),AB=CD=5,连接AC、BD、BC,将△ABC沿BC折叠得到△A1BC.
(1)求四边形ABDC的面积.
(2)当A1与D重合时,四边形ABDC是什么特殊四边形,为什么?
(3)当A1与D不重合时:①连接A1、D,求证:A1D∥BC;②若以A1,B,C,D为顶点的四边形为矩形,且矩形的边长分别为a,b,求(a+b)2的值.
参考答案:
【答案】(1)10;(2)四边形ABDC是菱形;(3)①证明见解析;②45或49.
【解析】(1)根据平行四边形的判定方法可得到四边形ABCD为平行四边形,然后根据平行四边形的面积公式计算;
(2)根据折叠的性质得到AC=CD,然后根据菱形的判定方法可判断四边形ABDC是菱形;
(3)①连结A1D,根据折叠性质和平行四边形的性质得到CA1=CA=BD,AB=CD=A1B,∠1=∠CBA=∠2,可证明△A1CD≌△A1BD,则∠3=∠4,然后利用三角形内角和定理得到得到∠1=∠4,则根据平行线的判定得到A1D∥BC;
②讨论:当∠CBD=90°,则∠BCA=90°,由于S△A1CB=S△ABC=5,则S矩形A1CBD=10,即ab=10,由BA1=BA=5,根据勾股定理得到a2+b2=25,然后根据完全平方公式进行计算;
当∠BCD=90°,则∠CBA=90°,易得BC=2,而CD=5,所以(a+b)2=(2+5)2.
解(1)∵AB=CD=5,AB∥CD,
∴四边形ABCD为平行四边形,
∴四边形ABDC的面积=2×5=10;
(2)∵四边形ABDC是平行四边形,
∵A1与D重合时,
∴AC=CD,
∵四边形ABDC是平行四边形,
∴四边形ABDC是菱形;
(3)①连结A1D,如图所示,
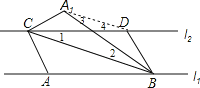
∵△ABC沿BC折叠得到△A1BC,
∴CA1=CA=BD,AB=CD=A1B,
在△A1CD和△A1BD中
CA1=BD,CD=BA1,A1D=A1D,
∴△A1CD≌△A1BD(SSS),
∴∠3=∠4,
又∵∠1=∠CBA=∠2,
∴∠1+∠2=∠3+∠4,
∴∠1=∠4,
∴A1D∥BC;
②当∠CBD=90°,
∵四边形ABDC是平行四边形,
∴∠BCA=90°,
∴S△A1CB=S△ABC=![]() ×2×5=5,
×2×5=5,
∴S矩形A1CBD=10,即ab=10,
而BA1=BA=5,
∴a2+b2=25,
∴(a+b)2=a2+b2+2ab=45;
当∠BCD=90°时,
∵四边形ABDC是平行四边形,
∴∠CBA=90°,
∴BC=2,
而CD=5,
∴(a+b)2=(2+5)2=49,
∴(a+b)2的值为45或49.
“点睛”本题考查了四边形综合题:熟练掌握平四边形的判定与性质以及特殊平行四边形的判定与性质;会运用折叠的性质确定相等的线段和角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
 (a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
A. 2a﹣b=0
B. a+b+c>0
C. 3a﹣c=0
D. 当a=
 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定的角度后得到△DBE,且使点D落在y轴上,与此同时顶点E恰好落在y=
 的图象上,则k的值为( )
的图象上,则k的值为( )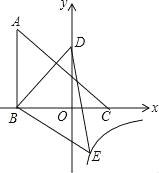
A.-3 B.-4 C.-5 D.-3
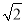
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式成立的是( )
A. (ab)10÷(ab)5=a2b2 B. (x+2)2=x2+4
C. (a3)2a2=a8 D. 2x4+3x4=5x8
-
科目: 来源: 题型:
查看答案和解析>>【题目】校学生会体育部为更好的开展同学们课外体育活动,现对学生最喜欢的一项球类运动进行了随机抽样调查,根据调查的结果绘制成如图①和②所示的两幅不完整的统计图,其中 A.喜欢篮球 B.喜欢足球 C.喜欢乒乓球,D.喜欢排球,请你根据统计图提供的信息,完成下列问题:

(1)本次一共调查了 名学生;
(2)把图①汇总条形统计图补充完整;
(3)求图②中表示“D.喜欢排球”部分所在扇形的圆心角的度数;
(4)若该校有3000名学生,请你估计全校可能有多少名学生喜欢足球运动.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A:从不闯红灯;B:偶尔闯红灯;C:经常闯红灯;D:其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:

(1)本次调查共选取名居民;
(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;
(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. a8÷a2=a4 B. a3a2=a6 C. (﹣2a3)2=4a9 D. 6x23xy=18x3y
相关试题

