【题目】如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
![]()
(1)当t=2时,①AB= ___ cm.②求线段CD的长度.
(2)用含t的代数式表示运动过程中AB的长.
(3)在运动过程中,若AB中点为E,则EC的长是否变化?若不变,求出EC的长;若发生变化,请说明理由.
参考答案:
【答案】(1)①4;②3;(2)①当![]() 时,
时, ![]() ,②当
,②当![]() 时,
时, ![]() ;(3)在运动过程中EC的长保持不变,恒等于5.
;(3)在运动过程中EC的长保持不变,恒等于5.
【解析】试题分析:(1)①根据AB=2t即可得出结论;
②先求出BD的长,再根据C是线段BD的中点即可得出CD的长;
(2)根据AB=2t即可得出结论;
(3)直接根据中点公式即可得出结论.
试题解析:(1)当t=2时,①AB= 4 cm.
②解:∵![]()
又∵![]() ,
, ![]()
∴![]()
∵点C是线段BD的中点
∴![]()
(2)①当![]() 时,此时点B从A向D移动:
时,此时点B从A向D移动: ![]()
②当![]() 时,此时点B从D向A移动:
时,此时点B从D向A移动: ![]()
(3)①当![]() 时,此时点B从A向D移动:
时,此时点B从A向D移动:
∵点E是AB的中点, ![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∵点C是BD的中点
∴![]()
又∵![]()
∴![]()
②当![]() 时,此时点B从D向A移动:
时,此时点B从D向A移动:
∵点E是AB的中点, ![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∵点C是BD的中点
∴![]()
又∵![]()
∴![]()
综上所述:在运动过程中EC的长保持不变,恒等于5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=
 BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=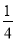 BC 成立的个数有( )
BC 成立的个数有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )

A.
B.
C.

D.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab

D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明有5张写着不同数的卡片,请你分别按要求抽出卡片,写出符合要求的算式:

(1)从中取出2张卡片,使这2张卡片上的数的乘积最大;
(2)从中取出2张卡片,使这2张卡片上的数相除的商最小;
(3)从中取出2张卡片,使这2张卡片上的数通过有理数的运算后得到的结果最大;
(4)从中取出4张卡片,使这4张卡片通过有理数的运算后得到的结果为24.(写出一种即可)
相关试题

