【题目】如图,直线y=k1x+7(k1<0)与x轴交于点A,与y轴交于点B,与反比例函数y= ![]() (k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为
(k2>0)的图象在第一象限交于C、D两点,点O为坐标原点,△AOB的面积为 ![]() ,点C横坐标为1.
,点C横坐标为1. 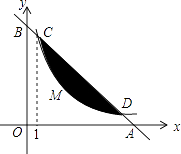
(1)求反比例函数的解析式;
(2)如果一个点的横、纵坐标都是整数,那么我们就称这个点为“整点”,请求出图中阴影部分(不含边界)所包含的所有整点的坐标.
参考答案:
【答案】
(1)解:∵当x=0时,y=7,当y=0时,x=﹣ ![]() ,
,
∴A(﹣ ![]() ,0)、B(0、7).
,0)、B(0、7).
∴S△AOB= ![]() |OA||OB|=
|OA||OB|= ![]() ×(﹣
×(﹣ ![]() )×7=
)×7= ![]() ,解得k1=﹣1.
,解得k1=﹣1.
∴直线的解析式为y=﹣x+7.
∵当x=1时,y=﹣1+7=6,
∴C(1,6).
∴k2=1×6=6.
∴反比例函数的解析式为y= ![]()
(2)解:∵点C与点D关于y=x对称,
∴D(6,1).
当x=2时,反比例函数图象上的点为(2,3),直线上的点为(2,5),此时可得整点为(2,4);
当x=3时,反比例函数图象上的点为(3,2),直线上的点为(3,4),此时可得整点为(3,3);
当x=4时,反比例函数图象上的点为(4, ![]() ),直线上的点为(4,3),此时可得整点为(4,2);
),直线上的点为(4,3),此时可得整点为(4,2);
当x=5时,反比例函数图象上的点为(5, ![]() ),直线上的点为(5,2),此时,不存在整点.
),直线上的点为(5,2),此时,不存在整点.
综上所述,符合条件的整点有(2,4)、(3,3)、(4,2)
【解析】(1)分别令x=0、y=0,求得对应y和x的值,从而的得到点A、B的坐标,然后依据三角形的面积公式可求得k1的值,然后由直线的解析式可求得点C的坐标,由点C的坐标可求得反比例函数的解析式;(2)由函数的对称性可求得D(6,1),从而可求得x的值范围,然后求得当x=2、3、4、5时,一次函数和反比例函数对应的函数值,从而可得到整点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点 A 表示的有理数为﹣4,点 B 表示的有理数为 6,点 P 从 点 A 出发以每秒 2 个单位长度的速度在数轴上沿由 A 到 B 方向运动,当点 P 到 达点 B 后立即返回,仍然以每秒 2 个单位长度的速度运动至点 A 停止运动.设 运动时间为 t(单位:秒).
(1)求 t=2 时点 P 表示的有理数;
(2)求点 P 是 AB 的中点时 t 的值;
(3)在点 P 由点 A 到点 B 的运动过程中,求点 P 与点 A 的距离(用含 t 的代数式表示);
(4)在点 P 由点 B 到点 A 的返回过程中,点 P 表示的有理数是多少(用含 t 的 代数式表示).
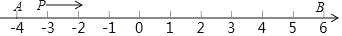
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O直径,C为⊙O上一点,点D是
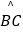 的中点,DE⊥AC于E,DF⊥AB于F.
的中点,DE⊥AC于E,DF⊥AB于F. 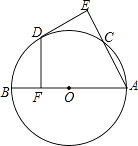
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若OF=4,求AC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24【题目】乘法公式的探究及应用.
探究问题
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.


(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
 =________;
=________;  =________.
=________.拓展运用:
(5)计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】绵阳人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
相关试题

