【题目】如图，Rt△ABC的斜边AB在x轴上，AB＝4，点B的坐标为（－1，0），点C在y轴的正半轴．若抛物线的图象经过点A，B，C．

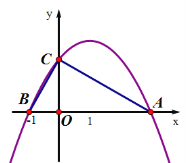
（Ⅰ）求y关于x的函数解析式；

（Ⅱ）设对称轴与抛物线交于点E，与AC交于点D。在对称轴上，是否存在点P，使以点P、C、D为顶点的三角形与ΔADE相似？若存在，请求出点P的坐标；若不存在，请说明理由。

（Ⅲ）若在对称轴上有两个动点P和Q（点P在点Q的上方），且PQ=，请求出使四边形BCPQ周长最小的点P的坐标．

参考答案：

【答案】(Ⅰ) y=（Ⅱ）（1，-）；（1，） （Ⅲ）P（1，）

【解析】

试题分析：(Ⅰ) 根据抛物线的对称性确定出点A（3,0），设y=a(x+1)(x-3)，利用相似三角形求出线段OC=,得出C（0，），然后把点C的坐标代入函数解析式求出a的值即可，（Ⅱ）求出点E、D的坐标，然后分①当点P在D下方，②当点P在D下方，两种情况讨论，利用相似三角形的性质可分别确定出点P的坐标；（Ⅲ）确定点C关于对称轴x=1的对称点C’（2，），过点B作BF⊥x轴，求出直线直线FC’的解析式，令x=1，可求出满足条件的点P的坐标.

试题解析：(Ⅰ)∵AB=4,B(-1,0)， ∴OA=3，点A（3,0）

易算得OC=,∴C（0，）

设y=a(x+1)(x-3)，把点C的坐标代入函数解析式，得a=

∴y=

(Ⅱ)由y=得抛物线的对称轴为直线x=1.

当x=1时，y=,∴E(1, )

设直线AC的解析式为y=kx+b,由A（3,0），C（0，）

求得y=

当x=1时，y=,∴D(1, ),则DE=

设对称轴交x轴于H点，则DH=.

在直角三角形ACO和ADP中，易求得AC=2,AD=,∴DC=.

①当点P在D下方，且DP=DA=时，ΔPDC≌ΔADE。

此时，点P的坐标为（1，-）

②当点P在D下方，且时，ΔCDP∽ΔADE，解得DP=.

此时，点P的坐标为（1，）

（Ⅲ）作点C关于对称轴x=1的对称点C’，则C’（2，）。

过点B作BF⊥x轴，使BF=PQ=，则F（-1，）,

连结FC’，交对称轴于点P。点P就为所求的点。

设直线FC’的解析式为y=mx+n。

将点C’（2，）和F（-1，）代入y=mx+n得m=

∴y=。

当x=1时，y=, 即P（1，）

关闭