搜索
【题目】小明购买双色球福利彩票时，两次分别购买了1张和100张，均未获奖，于是他说：“购买1张和100张中奖的可能性相等．”小华说：“这两个事件都是不可能事件．”他们的说法对吗？请说明理由．
参考答案：
【答案】答：小明的说法错误，因为买100张中奖的可能性比买1张的中奖可能性大，小华的说法错误，这两个事件都是随机事件不能因为事件发生的可能性小就认为它是不可能事件．
【解析】小明的说法错误，因为买100张中奖的可能性比买1张的中奖可能性大，小华的说法错误，这两个事件都是随机事件不能因为事件发生的可能性小就认为它是不可能事件．
此题主要考查了随机事件的意义，正确理解随机事件的意义是解题关键．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在下面给出的数轴中A表示1，B表示﹣2.5，回答下面的问题：
（1）A、B之间的距离是
（2）观察数轴，与点A的距离为5的点表示的数是： ；
（3）若将数轴折叠，使A点与﹣2表示的点重合，则B与数 表示的点重合
（4）若数轴上M、N两点之间的距离为2016（M在N的左侧），且M、N两点经过（3）中折叠后互相重合，则M、N两点表示的数分别是：M： N： ．
-
科目： 来源： 题型：
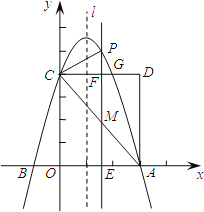
查看答案和解析>>【题目】如图，抛物线
（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G．（1）求抛物线的解析式；
（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；
（3）在（2）的条件下，连结PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次函数y=2x+4的图象与y轴交点的坐标是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】单项式﹣3xy2z3的系数和次数分别是（ ）
A. ﹣3，5 B. ﹣3，8 C. ﹣3，7 D. ﹣3，6
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣3，0）、B（5，0）、C（0，5）三点，O为坐标原点
（1）求此抛物线的解析式；
（2）若把抛物线y=ax2+bx+c（a≠0）向下平移
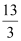个单位长度，再向右平移n（n＞0）个单位长度得到新抛物线，若新抛物线的顶点M在△ABC内，求n的取值范围；（3）设点P在y轴上，且满足∠OPA+∠OCA=∠CBA，求CP的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题是真命题的是（ ）
A.在一个三角形中，至多有两个内角是钝角
B.三角形的两边之和小于第三边
C.在一个三角形中，至多有两个内角是锐角
D.在同一平面内，垂直于同一直线的两直线平行
相关试题
