【题目】如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH. 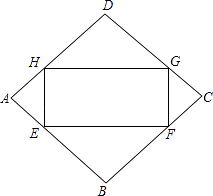
(1)求证:四边形EFGH是矩形;
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的面积最大?
参考答案:
【答案】
(1)证明:∵DG=DH,
∴∠DHG=∠DGH= ![]() ,
,
同理,∠CGF= ![]() ,
,
∴∠DGH+∠CGF= ![]() ,
,
又∵菱形ABCD中,AD∥BC,
∴∠D+∠C=180°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理,∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(2)解:AB=a,∠A=60°,则菱形ABCD的面积是: ![]() a2,
a2,
设BE=x,则AE=a﹣x,
则△AEH的面积是: ![]() ,
,
△BEF的面积是: ![]() ,
,
则矩形EFGH的面积y= ![]() a2﹣
a2﹣ ![]() ﹣
﹣ ![]() ,
,
即y=﹣ ![]() x2+
x2+ ![]() ax,
ax,
则当x= ![]() =
= ![]() 时,函数有最大值.
时,函数有最大值.
此时BE= ![]() .
.
【解析】(1)利用等腰三角形的性质:等边对等角,以及平行线的性质可以证得∠DGH+∠CGH=90°,则∠HGF=90°,根据三个角是直角的四边形是矩形,即可证得;(2)设BE的长是x,则利用x表示出矩形EFGH的面积,根据函数的性质即可求解.
【考点精析】通过灵活运用二次函数的最值和菱形的性质,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顾琪在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是她在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
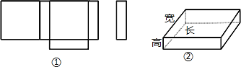
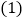 顾琪总共剪开了________条棱.
顾琪总共剪开了________条棱. 现在顾琪想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为她应该将剪断的纸条粘贴到①中的什么位置?请你帮助她在①上补全.
现在顾琪想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为她应该将剪断的纸条粘贴到①中的什么位置?请你帮助她在①上补全. 已知顾琪剪下的长方体的长、宽、高分别是
已知顾琪剪下的长方体的长、宽、高分别是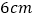 、
、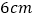 、
、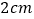 ,求这个长方体纸盒的体积.
,求这个长方体纸盒的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE.
(下面请你完成余下的证明过程)


(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正
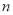 边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD……X”,请你作出猜想:当∠AMN= °时,结论AM=MN仍然成立.(直接写出答案,不需要证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图
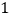 ,大正方体上截去一个小正方体后,可得到图
,大正方体上截去一个小正方体后,可得到图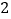 的几何体.
的几何体.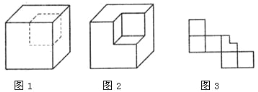
 设原大正方体的表面积为
设原大正方体的表面积为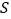 ,图
,图 中几何体的表面积为
中几何体的表面积为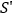 ,那么
,那么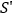 与
与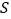 的大小关系是( )
的大小关系是( )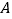 、
、
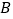 、
、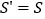
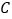 、
、
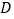 、不确定
、不确定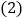 小明说:“设图
小明说:“设图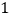 中大正方体各棱的长度之和为
中大正方体各棱的长度之和为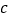 ,图
,图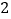 中几何体各棱的长度之和为
中几何体各棱的长度之和为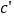 ,那么
,那么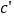 比
比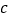 正好多出大正方体
正好多出大正方体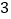 条棱的长度.”若设大正方体的棱长为
条棱的长度.”若设大正方体的棱长为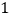 ,小正方体的棱长为
,小正方体的棱长为 ,请问
,请问 为何值时,小明的说法才正确?
为何值时,小明的说法才正确? 如果截去的小正方体的棱长为大正方体棱长的一半,那么图
如果截去的小正方体的棱长为大正方体棱长的一半,那么图 是图
是图 中几何体的表面展开图吗?如有错误,请在图
中几何体的表面展开图吗?如有错误,请在图 中修正.
中修正. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )
A. 495 B. 497 C. 501 D. 503
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为ɑ.
(1)如图1,若ɑ=90°,求AA′的长;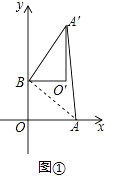
(2)如图2,若ɑ=120°,求点O′的坐标.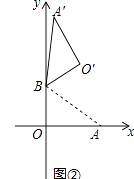
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
相关试题

