【题目】如图,已知![]() ,
,![]() 、
、![]() 的交点为
的交点为![]() ,现作如下操作:
,现作如下操作:
第一次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第二次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
第三次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() ,
,
…
第![]() 次操作,分别作
次操作,分别作![]() 和
和![]() 的平分线,交点为
的平分线,交点为![]() .
.
若![]() 度,那
度,那![]() 等于__________度.
等于__________度.


参考答案:
【答案】![]()
【解析】
先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;根据∠ABE和∠DCE的平分线交点为E1,则可得出∠CE1B=∠ABE1+∠DCE1![]() ∠ABE
∠ABE![]() ∠DCE
∠DCE![]() ∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2
∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2![]() ∠ABE1
∠ABE1![]() ∠DCE1
∠DCE1![]() ∠CE1B
∠CE1B![]() ∠BEC;根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C
∠BEC;根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C![]() ∠BEC;…据此得到规律∠En
∠BEC;…据此得到规律∠En![]() ∠BEC,最后求得∠BEC的度数.
∠BEC,最后求得∠BEC的度数.
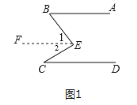
如图1,过E作EF∥AB.
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2.
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图2.
∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1![]() ∠ABE
∠ABE![]() ∠DCE
∠DCE![]() ∠BEC.
∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2![]() ∠ABE1
∠ABE1![]() ∠DCE1
∠DCE1![]() ∠CE1B
∠CE1B![]() ∠BEC;
∠BEC;
∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3![]() ∠ABE2
∠ABE2![]() ∠DCE2
∠DCE2![]() ∠CE2B
∠CE2B![]() ∠BEC;
∠BEC;
…
以此类推,∠En![]() ∠BEC,
∠BEC,
∴当∠En=1度时,∠BEC等于2n度.
故答案为:2n.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DEF是△ABC经过平移得到的.已知∠A=54°,∠ABC=36°,则下列结论不一定成立的是( )

A. ∠F=90° B. ∠BED=∠FED C. BC⊥DF D. DF∥AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△AOB中,两直角边OA,OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数
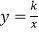 的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=4,tan∠BAO=2,则k的值为( )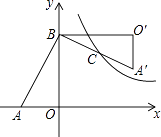
A.3
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠C=90°,D为AB的中点,E、F分别在AC、BC上,且DE⊥DF.
求证:AE2+BF2=EF2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,分别以点A和点B为圆心,大于
 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=45°,点D在边BC上,AD=AC,点E在边AD上,∠BCE=45°,若AB=5
 .AE=2DE,则AC= .
.AE=2DE,则AC= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
相关试题

