搜索
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列说法不正确的是（ ）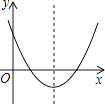 
A.b2﹣4ac＞0
B.a＞0
C.c＞0
D.
参考答案：
【答案】D
【解析】解：A、正确，∵抛物线与x轴有两个交点，∴△=b2﹣4ac＞0； B、正确，∵抛物线开口向上，∴a＞0；
C、正确，∵抛物线与y轴的交点在y轴的正半轴，∴c＞0；
D、错误，∵抛物线的对称轴在x的正半轴上，∴﹣ 
＞0．
故选：D．
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解中学课堂教学质量，我市教体局去年对全市中学教学质量进行调查
方法是通过考试
参加考试的为全市八年级学生
，从中随机抽取600名学生的英语成绩进行分析对于这次调查，以下说法不正确的是( )A. 调查方法是抽样调查 B. 全市八年级学生是总体
C. 参加考试的每个学生的英语成绩是个体 D. 被抽到的600名学生的英语成绩是样本
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC中，∠ACB=90°，BC=2，∠A=30°，点E，F分别是线段BC，AC的中点，连接EF．
（1）说明线段BE与AF的位置关系和数量关系；
（2）如图②，当△CEF绕点C顺时针旋转α（0°＜α＜90°）时，连接AF，BE，（1）中的结论是否仍然成立？如果成立，请证明；如果不成立，请说明理由；
（3）如图③，当△CEF绕点C顺时针旋转α（0°＜α＜180°）时，延长FC交AB于点D，如果AD=6﹣2
，求旋转角α的度数． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+2经过A（﹣1，0），B（2，0），C三点．直线y=mx+
交抛物线于A，Q两点，点P是抛物线上直线AQ上方的一个动点，作PF⊥x轴，垂足为F，交AQ于点N．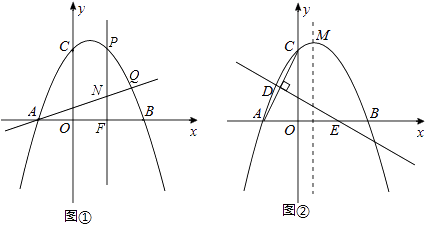
（1）求抛物线的解析式；
（2）如图①，当点P运动到什么位置时，线段PN=2NF，求出此时点P的坐标；
（3）如图②，线段AC的垂直平分线交x轴于点E，垂足为D，点M为抛物线的顶点，在直线DE上是否存在一点G，使△CMG的周长最小？若存在，请求出点G的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，动点S从点A出发，沿线段AB运动至点B后，立即按原路返回，点S在运动过程中速度不变，则以点B为圆心，线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于一次函数y=kx+b，当自变量x的取值为﹣2≤x≤5时，相应的函数值的范围为﹣6≤y≤﹣3，则该函数的解析式为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程：
（1）x+2（5﹣3x）=15﹣3（7﹣5x）
（2）
（3）
（4）
．
相关试题
