搜索
【题目】如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）
A. 40° B. 45° C. 60° D. 70°
参考答案：
【答案】A
【解析】
根据平行线的性质可得∠CBD的度数，根据角平分线的性质可得∠CBA的度数，根据等腰三角形的性质可得∠C的度数，根据三角形内角和定理可得∠BAC的度数．
解：∵AE∥BD，∴∠CBD=∠E=35°，∵BD平分∠ABC，∴∠CBA=70°，∵AB=AC，
∴∠C=∠CBA=70°，∴∠BAC=180°﹣70°×2=40°．
故选A．
“点睛”考查了平行线的性质，角平分线的性质，等腰三角形的性质和三角形内角和定理．关键是得到∠C=∠CBA=70°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形ABCD中，E、F分别是CD、BC上的点．若∠AEF=90°，则一定有（ ）
A.△ADE∽△ECF
B.△BCF∽△AEF
C.△ADE∽△AEF
D.△AEF∽△ABF -
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图，其对称轴为直线x=﹣1，给出下列结果：（1）b2＞4ac；（2）abc＞0；（3）2a+b=0；（4）a+b+c＞0；（5）a﹣b+c＜0．
则正确的结论是（ ）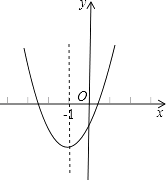
A.（1）（2）（3）（4）
B.（2）（4）（5）
C.（2）（3）（4）
D.（1）（4）（5） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
【答案】证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边)，
在△ABF和△ACF中，
，∴△ABF≌△ACF(SSS)，
∴∠BAF=∠CAF(全等三角形对应角相等)，
∴AF平分∠BAC.
【题型】解答题
【结束】
23【题目】如图，在△ABC中，AC=BC，∠C=90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．
（1）求证：CD=BE；
（2）已知CD=2，求AC的长；
（3）求证：AB=AC+CD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AD是△ABC的高，∠BAC=60°，BD=2CD=2，试求AB的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，某数学兴趣小组的同学利用标杆测量旗杆（AB）的高度：将一根5米高的标杆（EF）竖在某一位置，有一名同学站在一处与标杆、旗杆成一条直线，此时他看到标杆顶端与旗杆顶端重合，另外一名同学测得站立的同学离标杆3米，离旗杆30米．如果站立的同学的眼睛距地面（CD）1.6米，求旗杆的高度．
-
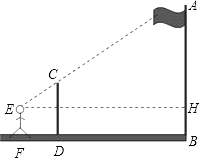
科目： 来源： 题型：
查看答案和解析>>【题目】某商场计划购进
，
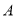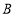两种新型节能台灯共100盏，这两种台灯的进价、售价如下表：类型
价格
进价（元/盏）
售价（元/盏）
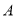型30
45
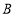型50
70
（1）若设商场购进
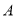型台灯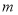
盏，销售完这批台灯所获利润为
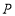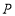，写出与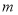之间的函数关系式；（2）若商场规定
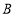型灯的进货数量不超过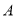型灯数量的4倍，那么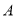型和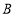型台灯各进多少盏售完之后获得利润最多？此时利润是多少元．
相关试题
