【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
两种新型节能台灯共100盏,这两种台灯的进价、售价如下表:
类型 | 价格 | 进价(元/盏) | 售价(元/盏) |
| 30 | 45 | |
| 50 | 70 | |
(1)若设商场购进![]() 型台灯
型台灯![]() 盏,销售完这批台灯所获利润为
盏,销售完这批台灯所获利润为![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若商场规定![]() 型灯的进货数量不超过
型灯的进货数量不超过![]() 型灯数量的4倍,那么
型灯数量的4倍,那么![]() 型和
型和![]() 型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
型台灯各进多少盏售完之后获得利润最多?此时利润是多少元.
参考答案:
【答案】(1)![]() ;(2)购进
;(2)购进![]() 型台灯20盏,
型台灯20盏,![]() 型台灯80盏时获利最多,利润为
型台灯80盏时获利最多,利润为![]() 元.
元.
【解析】
(1)由商场购进A型台灯m盏,得出购进B型台灯为(100m)盏,然后根据题意列出函数解析式即可;
(2)设商场销售完这批台灯可获利P元,根据获利等于两种台灯的获利总和列式整理,再求出m的取值范围,然后根据一次函数的增减性求出获利的最大值.
解:(1)因为商场购进A型台灯m盏,则购进B型台灯为(100m)盏,由题意可得:
![]() ,
,
![]()
![]() ,
,
所以![]() 与
与![]() 之间的函数关系式:
之间的函数关系式:![]() ;
;
(2)![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的4倍,由题意得:
型台灯数量的4倍,由题意得:
![]() ,
,
解得:![]() ,
,
![]() ,
,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
∴当![]() 时,
时,![]() 取得最大值,为
取得最大值,为![]() (元),此时100m=80.
(元),此时100m=80.
答:商场购进![]() 型台灯20盏,
型台灯20盏,![]() 型台灯80盏,销售完这批台灯时获利最多,此时利润为
型台灯80盏,销售完这批台灯时获利最多,此时利润为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的高,∠BAC=60°,BD=2CD=2,试求AB的长.

-
科目: 来源: 题型:
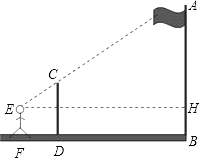
查看答案和解析>>【题目】如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

-
科目: 来源: 题型:
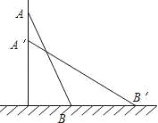
查看答案和解析>>【题目】如图,一架梯子AB长13米,斜靠在一面墙上,梯子底端离墙5米.(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了5米,那么梯子的底端在水平方向滑动了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )

A. =
= 
B. =
= 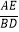
C. =
= 
D. =
= 
相关试题

