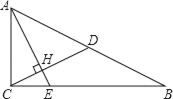
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
参考答案:
【答案】(1)![]() ;(2)3.
;(2)3.
【解析】
试题(1)根据∠ACB=90°,CD是斜边AB上的中线,可得出CD=BD,则∠B=∠BCD,再由AE⊥CD,可证明∠B=∠CAH,由AH=2CH,可得出CH:AC=1:![]() ,即可得出sinB的值;
,即可得出sinB的值;
(2)根据sinB的值,可得出AC:AB=1:![]() ,再由AB=
,再由AB=![]() ,得AC=2,则CE=1,从而得出BE.
,得AC=2,则CE=1,从而得出BE.
试题解析:(1)∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=BD,
∴∠B=∠BCD,
∵AE⊥CD,
∴∠CAH+∠ACH=90°,
又∠ACB=90°,
∴∠BCD+∠ACH=90°,
∴∠B=∠BCD=∠CAH,即∠B=∠CAH,
∵AH=2CH,
∴由勾股定理得AC=![]() CH,
CH,
∴CH:AC=1:![]() ,
,
∴sinB=![]() ;
;
(2)∵sinB=![]() ,
,
∴AC:AB=1:![]() ,
,
∴AC=2.
∵∠CAH=∠B,
∴sin∠CAH=sinB=![]() =
=![]() ,
,
设CE=x(x>0),则AE=![]() x,则
x,则![]() ,
,
∴CE=x=1,AC=2,
在Rt△ABC中,![]() ,
,
∵AB=2CD=![]() ,
,
∴BC=4,
∴BE=BC﹣CE=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学生本学期6次数学考试成绩如下表所示:
成绩类别
第一次月考
第二次月考
期中
第三次月考
第四次月考
期末
成绩/分
105
110
108
113
108
112
(1)6次考试成绩的中位数为 ,众数为 .
(2)求该生本学期四次月考的平均成绩.
(3)如果本学期的总评成绩按照月考平均成绩占20﹪、期中成绩占30﹪、期末成绩占50﹪计算,那么该生本学期的数学总评成绩是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒4°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒6°的速度旋转,直线MN保持不动,如图2,设旋转时间为t(0≤t≤60,单位:秒).
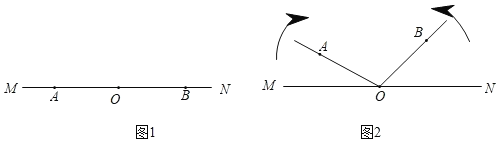
(1)当t=3时,求∠AOB的度数;
(2)在运动过程中,当∠AOB第二次达到72°时,求t的值;
(3)在旋转过程中是否存在这样的t,使得射线OB与射线OA垂直?如果存在,请求出t的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A,B分别在x轴,y轴上,点A的坐标为(﹣1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动,如果PQ=
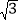 ,那么当点P运动一周时,点Q运动的总路程为__________.
,那么当点P运动一周时,点Q运动的总路程为__________.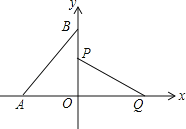
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究函数
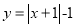 的图象与性质.
的图象与性质.小明根据学习函数的经验,对函数
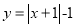 的图象与性质进行了研究.
的图象与性质进行了研究.下面是小明的研究过程,请补充完成.
(1)自变量
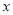 的取值范围是全体实数,
的取值范围是全体实数,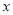 与
与 的几组对应值列表如下:
的几组对应值列表如下: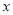
…
-4
-3
-2
-1
0
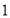

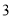
4
…

…
2
1
0
n
0
1
m
3
4
…
其中,m= n= ;
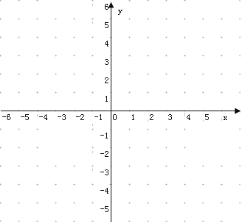
(2)在如图所示的平面直角坐标中,描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象.
(3)观察图象,写出该函数的两条性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=
 S△BOC,求点D的坐标.
S△BOC,求点D的坐标.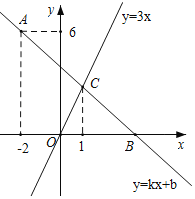
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
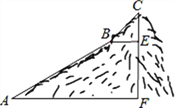
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(
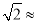 1.414,CF结果精确到米)
1.414,CF结果精确到米)
相关试题

