【题目】拓展与探索:如图,在正△ABC中,点E在AC上,点D在BC的延长线上.
(1)如图1,AE=EC=CD,求证:BE=ED;
(2)如图2,若E为AC上异于A、C的任一点,AE=CD,(1)中结论是否仍然成立?为什么?
(3)若E为AC延长线上一点,且AE=CD,试探索BE与ED间的数量关系,并证明你的结论.

参考答案:
【答案】(1)证明见解析;(2)成立,理由见解析;(3)BE=ED,证明见解析.
【解析】
(1)根据等边三角形的性质得到∠EBC=![]() ∠ABC=30°,根据等腰三角形的判定定理证明;
∠ABC=30°,根据等腰三角形的判定定理证明;
(2)过点E作EF∥BC,证明△EFB≌△DCE,根据全等三角形的性质证明;
(3)过点E作EF∥AB,证明△BCE≌△DFE,根据全等三角形的性质证明.
解:(1)∵△ABC是等边三角形,AE=CE,
∴BE平分∠ABC,
∴∠EBC=![]() ∠ABC=30°,
∠ABC=30°,
∵∠ACB=60°,
∴∠ECD=120°,
∵CE=CD,
∴∠D=∠CED=30°,
∴∠EBC=∠D=30°,
∴BE=ED;
(2)成立,
理由如下:过点E作EF∥BC,交AB于F,
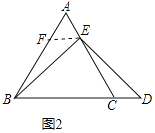
∵△ABC是等边三角形,
∴△AEF是等边三角形,AF=AE=EF,
∴∠BFE=∠ECD=120°,BF=EC,
∵AE=CD,
∴EF=CD,
在△EFB和△DCE中,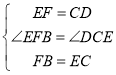 ,
,
∴△EFB≌△DCE(SAS)
∴BE=ED;
(3)结论:BE=ED.
理由如下:如图3,过点E作EF∥AB,交CD于F,
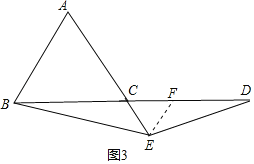
则△CEF是等边三角形,
∴CF=CE=EF,∠BCE=∠DFE=120°,
∵AE=CD,
∴AE﹣CE=CD﹣CF,即AC=FD,
∵AC=BC,
∴BC=FD,
在△BCE和△DFE中,
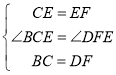 ,
,
∴△BCE≌△DFE(SAS),
∴BE=ED.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)求证:MN=AM+BN.
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.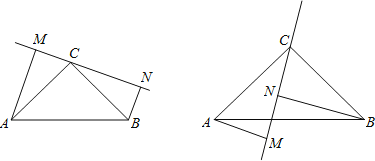
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
课外兴趣小组活动时,老师提出了如下问题:

如图1,△ABC中,若AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使DE=AD,请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB的理由是_____.
A.SSS B.SAS C.AAS D.HL
(2)求得AD的取值范围是______.
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
(感悟)
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
(3)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.求证:AC=BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完.销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示.下列结论正确的是( )

A.降价后西瓜的单价为2元/千克B.广宇一共进了50千克西瓜
C.售完西瓜后广宇获得的总利润为44元D.降价前的单价比降价后的单价多0.6元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,BD和CD为⊙O的切线,切点分别为B和C.
(1)求证:AC∥OD;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克)
…
34.8
32
29.6
28
…
售价 x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
相关试题

