【题目】已知数轴上有A,B,C三点,分别表示数﹣24,﹣10,10.两只电子蚂蚁甲、乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
(1)问甲、乙在数轴上的哪个点相遇?
(2)问多少秒后甲到A,B,C三点的距离之和为40个单位?.
(3)若甲、乙两只电子蚂蚁(用P表示甲蚂蚁、Q表示乙蚂蚁)分别从A,C两点同时相向而行,甲的速度变为原来的3倍,乙的速度不变,直接写出多少时间后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点.
![]()
参考答案:
【答案】解:(1)设x秒后甲与乙相遇,则4x+6x=34,
解得 x=3.4,
4×3.4=13.6,-24+13.6=-10.4.
故甲、乙在数轴上的-10.4相遇,故答案为:-10.4;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应位于AB或BC之间.
AB之间时:4y+(14-4y)+(14-4y+20)=40
解得y=2;
BC之间时:4y+(4y-14)+(34-4y)=40,
解得y=5.
甲从A向右运动2秒时返回,设y秒后与乙相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:-24+4×2-4y;乙表示的数为:10-6×2-6y,
依据题意得:-24+4×2-4y=10-6×2-6y,
解得:y=7,
相遇点表示的数为:-24+4×2-4y=-44(或:10-6×2-6y=-44),
②甲从A向右运动5秒时返回,设y秒后与乙相遇.
甲表示的数为:-24+4×5-4y;乙表示的数为:10-6×5-6y,
依据题意得:-24+4×5-4y=10-6×5-6y,
解得:y=-8(不合题意舍去),
即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.
(3)①设x秒后原点O是甲蚂蚁P与乙蚂蚁Q两点的中点,则
24-12x=10-6x,解得x=![]() ;
;
设x秒后乙蚂蚁Q是甲蚂蚁P与原点O两点的中点,则
24-12x=2(6x-10),解得x=![]() ;
;
设x秒后甲蚂蚁P是乙蚂蚁Q与原点O两点的中点,则
2(24-12x)=6x-10,解得x=![]() ;
;
综上所述,![]() 秒或
秒或![]() 秒或
秒或![]() 秒后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点.
秒后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点.
【解析】试题分析:(1)可设x秒后甲与乙相遇,根据甲与乙的路程差为34,可列出方程求解即可;(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应位于AB或BC之间两种情况讨论,即可求解.(3)分①原点O是甲蚂蚁P与乙蚂蚁Q两点的中点;②乙蚂蚁Q是甲蚂蚁P与原点O两点的中点;③甲蚂蚁P是乙蚂蚁Q与原点O两点的中点,三种情况讨论即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边长分别为4,5,x,则x不可能是( )
A.3
B.5
C.7
D.9 -
科目: 来源: 题型:
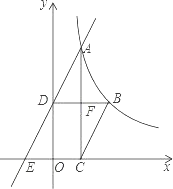
查看答案和解析>>【题目】如图,已知函数y=
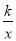 (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E(1)若AC=
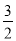 OD,求a、b的值;
OD,求a、b的值;(2)若BC∥AE,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多项式与3x2+9x的和等于3x2+4x-1,则这个多项式是( )
A. -5x-1 B. 5x+1 C. -13x-1 D. 13x+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】新化县城区2015年平均房价为每平方米2500元,连续两年增长后,2017年平均房价达到每平方米3500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
A. 3500(1+x)2=2500 B. 3500(1﹣x)2=2500 C. 2500(1﹣x)2=3500 D. 2500(1+x)2=3500
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的四个内角平分线围成的四边形( )
A. 一定是正方形 B. 是矩形
C. 菱形 D. 只能是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华和小丽最近测了自己的身高,小华量得自己约1.6m,小丽测得自己的身高约为1.60m,下列关于她俩身高的说法正确的是( )
(A)小华和小丽一样高;(B)小华比小丽高;(C)小华比小丽低;(D)无法确定谁高.
相关试题

