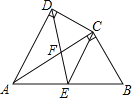
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F,AD=4,AB=6.
(1)求证:△ADC∽△ACB;
(2)求AC的值;
(3)求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)AC=2![]() ;(3)
;(3)![]() =
=![]() .
.
【解析】
试题分析:(1)根据两个角对应相等的两个三角形相似证明即可;
(2)根据相似三角形的对应边的比相等列出比例式,计算即可;
(3)根据直角三角形斜边上的中线是斜边的一半得到CE=AE,证明△AFD∽△CFE,根据相似三角形的性质解答即可.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB;
(2)解:∵△ADC∽△ACB,
∴![]() =
=![]() ,即AC2=ADAB=24,
,即AC2=ADAB=24,
解得,AC=2![]() ;
;
(3)解:∵E为AB的中点,
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA;
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
∴△AFD∽△CFE,
∴![]() =
=![]() ,
,
∵CE=![]() AB=3,AD=4,
AB=3,AD=4,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算6m3÷(﹣3m2)的结果是( )
A.﹣3m B.﹣2m C.2m D.3m
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界文化遗产长城总长约6 700 000m,用科学记数法可表示为( )
A.6.7×105m B.6.7×10﹣5m
C.6.7×106m D.6.7×10﹣6m
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式xa2﹣xb2因式分解的结果是 .
-
科目: 来源: 题型:
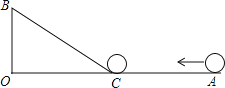
查看答案和解析>>【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若正多边形的内角和是540°,那么这个多边形一定是正 边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个外角都等于36°,则该多边形的内角和等于_______度.
相关试题

