【题目】(本题8分)如图1,平行四边形ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
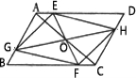
(1)求证:四边形EGFH是平行四边形;
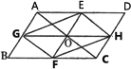
(2)如图2,若EF//AB,GH//BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
参考答案:
【答案】(1);(2)□ABFE、□GBCH、□EFCD、□EGFH
【解析】
试题分析:根据ABCD为平行四边形得出AD∥BC,则∠EAO=∠FCO,根据OA=OC,∠AOE=∠COF得出△OAE和△OCF全等,从而得出OE=OF,同理得出OG=OH,从而说明平行四边形;根据平行四边形的性质得出面积相等的四边形
试题解析:(1)证明:∵四边形ABCD为平行四边形 ∴AD∥BC ∴∠EAO=∠FCO
∵OA=OC ∠AOE=∠COF ∴△OAE≌△OCF ∴OE=OF 同理OG=OH ∴四边形EGFH是平行四边形
(2)□ABFE、□GBCH、□EFCD、□EGFH
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图,如图:
次数
频数
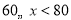
2
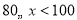
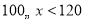
18
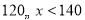
13
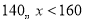
8
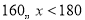
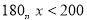
1
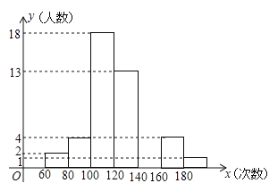
(1)补全频数分布表和频数分布直方图.
(2)上表中组距是__________次,组数是___________组.
(3)跳组次数在
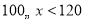 范围的学生有__________人,全班共有___________人.
范围的学生有__________人,全班共有___________人.(4)若规定跳维次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学决定在本校学生中开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.请你根据图中的信息,解答下列问题.

(1)m= ,n= ;
(2)请补全图中的条形图;
(3)扇形统计图中,足球部分的圆心角是 度;
(4)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,反比例函数y=
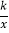 的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(
的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N( ,48)中,在该函数图象上的点有( )
,48)中,在该函数图象上的点有( )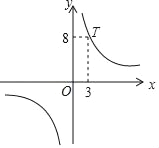
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.

请根据以上信息解答下列问题:
(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为________;
(2)请补全条形统计图;
(3)该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为1200×
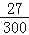 =108”,请你判断这种说法是否正确,并说明理由.
=108”,请你判断这种说法是否正确,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,矩形OABC的顶点O、A、C的坐标分别为O(0,0),A(﹣x,0),C(0,y),且x、y满足
 .
.(1)矩形的顶点B的坐标是 .
(2)若D是AB中点,沿DO折叠矩形OABC,使A点落在点E处,折痕为DO,连BE并延长BE交y轴于Q点.
①求证:四边形DBOQ是平行四边形.
②求△OEQ面积.
(3)如图2,在(2)的条件下,若R在线段AB上,AR=4,P是AB左侧一动点,且∠RPA=135°,求QP的最大值是多少?

相关试题

