【题目】如图,等边![]() 中,
中, ![]() 是
是![]() 的角平分线,
的角平分线, ![]() 为
为![]() 上一点,以
上一点,以![]() 为一边且在
为一边且在![]() 下方作等边
下方作等边![]() ,连接
,连接![]() .
.

(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )延长
)延长![]() 至
至![]() ,
, ![]() 为
为![]() 上一点,连接
上一点,连接![]() 、
、![]() 使
使![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
参考答案:
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )PQ=8.
)PQ=8.
【解析】试题分析:
(1)由△ABC、△DCE都是等边三角形可得:AC=BC、CD=CE,∠ACB=∠DCE=60°,从而可得∠ACD=∠BCE,这样由“SAS”即可证得:△ACD≌△BCE;
(2)由等边△ABC中,AO平分∠BAC可得∠CAD=![]() ∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=
∠BAC=30°,结合△ACD≌△BCE可得∠CBE=30°;过点C作CH⊥BQ于点H,由此可得CH=![]() BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
BC=3,在Rt△CHQ中,由勾股定理可得HQ=4,结合CP=CQ可得PQ=2HQ=8.
试题解析:
(![]() )∵
)∵![]() ,
, ![]() 均为等边三角形,
均为等边三角形,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
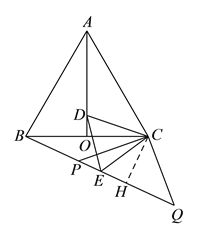
在![]() 和
和![]() 中,
中,
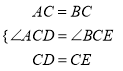 ,
,
∴![]() ≌
≌![]() .
.
(![]() )∵等边△ABC中,AO平分∠BAC,
)∵等边△ABC中,AO平分∠BAC,
∴∠CAD=![]() ∠BAC=30°.
∠BAC=30°.
如下图,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
由(![]() )知
)知![]() ≌
≌![]() ,
,
则![]() ,
,
∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
又∵CP=CQ,CH⊥PQ,
∴![]() .
.
-
科目: 来源: 题型:
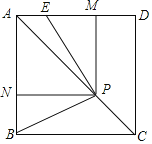
查看答案和解析>>【题目】如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
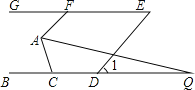
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过
 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方 m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为 m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点
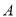 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为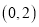 ,点
,点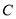 的坐标为
的坐标为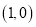 .
.(
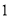 )在
)在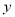 轴上是否存在点
轴上是否存在点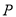 ,使
,使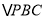 为等腰三角形,求出点
为等腰三角形,求出点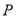 坐标.
坐标.(
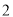 )在
)在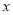 轴上方存在点
轴上方存在点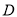 ,使以点
,使以点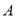 ,
, 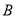 ,
, 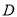 为顶点的三角形与
为顶点的三角形与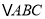 全等,画出
全等,画出 并请直接写出点
并请直接写出点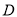 的坐标.
的坐标. -
科目: 来源: 题型:
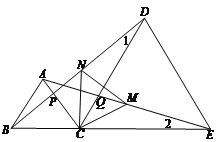
查看答案和解析>>【题目】线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.
(1)找出图中的所有全等三角形.
(2)找出一组相等的线段,并说明理由.
(3)取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知实数a、b在数轴上的位置如图所示,化简
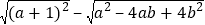 =_____________;
=_____________;
(2)已知正整数
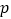 ,
, 满足
满足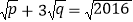 ,则整数对
,则整数对 的个数是_______________;
的个数是_______________;(3)△ABC中,∠A=50°,高BE、CF所在的直线交于点O,∠BOC的度数__________.
相关试题

