【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角项点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
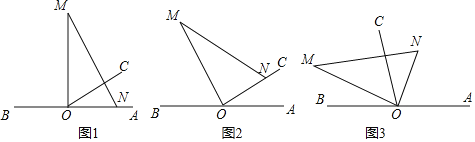
(1)将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周.如图2,经过t秒后,ON落在OC边上,则t= 秒(直接写结果).
(2)在(1)的条件下,若三角板继续转动,同时射线OC也绕O点以每秒10°的速度沿逆时针方向旋转一周,当OC转动9秒时,求∠MOC的度数.
(3)在(2)的条件下,它们继续运动多少秒时,∠MOC=35°?请说明理由.
参考答案:
【答案】(1)6;(2)∠MON=45°;(3)它们继续运动11秒或25时,∠MOC=35°.
【解析】
(1)根据:“角度=速度![]() 时间”进行计算,即可求得时间;
时间”进行计算,即可求得时间;
(2)当t=9时,可求得∠AOC和∠AON,通过计算角的差可求得答案;
(3)构造方程求解即可,注意分类讨论.
(1)由题意5t=30,解得t=6,
故答案为6.
(2)当t=9时,∠AOC=30°+9×10°=120°,∠AON=120°+9×5°=165°,
∴此时∠MON=∠AOC﹣∠AOM=165°﹣120°=45°.
(3)设继续运动t秒时,∠MOC=35°.
由题意:120°+5t﹣(30°+10t)=35°或30°+10t﹣(120°+5t)=35°
解得t=11或25.
∴它们继续运动11秒或25时,∠MOC=35°.
-
科目: 来源: 题型:
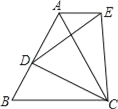
查看答案和解析>>【题目】如图,等边△ABC中,D是AB边上的一动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:△ACE≌△BCD;
(2)判断AE与BC的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
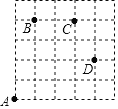
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中B→C( , )C→D( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】动手操作:
(1)如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD= 度;
(2)如图2,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
(3)灵活应用:请你直接利用以上结论,解决以下列问题:如图3,BE平分∠ABD,CE平分∠ACD,若∠BAC=40°,∠BDC=120°,求∠BEC的度数。



-
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2019按一定规律排列如下表:

平移表中带阴影的方框,则方框中五个数的和可以是
A.2010B.2018C.2019D.2020.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
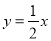 与双曲线y=
与双曲线y=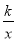 交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=
交于A、B两点,点B的坐标为(-4,-2),C为第一象限内双曲线y=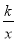 上一点,且点C在直线
上一点,且点C在直线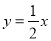 的上方.
的上方.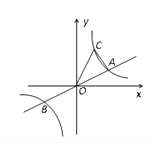
(1)求双曲线的函数解析式;
(2)若△AOC的面积为6,求点C的坐标.
-
科目: 来源: 题型:
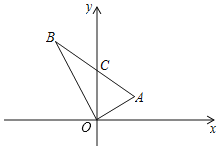
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为原点,点A(2,1),B(﹣2,4),直线AB与y轴交于点C.
(1)求点C的坐标;
(2)求证:△OAB是直角三角形.
相关试题

