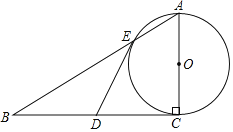
【题目】如图,已知Rt△ABC,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)求证:DE是⊙O的切线;
(2)若AE:EB=1:2,BC=12,求AE的长.
参考答案:
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OE、EC,根据已知条件易证∠1+∠3=∠2+∠4=90°,即可得∠OED=90°,所以DE是⊙O的切线;(2)证明△BEC∽△BCA,根据相似三角形的性质可得![]() ,即BC2=BEBA,设AE=x,则BE=2x,BA=3x,代入可得122=2x3x,解得x=2
,即BC2=BEBA,设AE=x,则BE=2x,BA=3x,代入可得122=2x3x,解得x=2![]() ,即可得AE=2
,即可得AE=2![]() .
.
(1)证明:连接OE、EC,
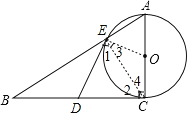
∵AC是⊙O的直径,
∴∠AEC=∠BEC=90°,
∵D为BC的中点,
∴ED=DC=BD,
∴∠1=∠2,
∵OE=OC,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,
即∠OED=∠ACB,
∵∠ACB=90°,
∴∠OED=90°,
∴DE是⊙O的切线;
(2)由(1)知:∠BEC=90°,
∵在Rt△BEC与Rt△BCA中,∠B=∠B,∠BEC=∠BCA,
∴△BEC∽△BCA,
∴![]() ,
,
∴BC2=BEBA,
∵AE:EB=1:2,设AE=x,则BE=2x,BA=3x,
∵BC=12,
∴122=2x3x,
解得:x=2![]() ,
,
即AE=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店老板准备购买A、B两种型号的足球共100只,已知A型号足球进价每只40元,B型号足球进价每只60元.
(1)若该店老板共花费了5200元,那么A、B型号足球各进了多少只;
(2)若B型号足球数量不少于A型号足球数量的
 ,那么进多少只A型号足球,可以让该老板所用的进货款最少?
,那么进多少只A型号足球,可以让该老板所用的进货款最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
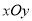 中,反比例函数
中,反比例函数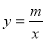 的图象与一次函数
的图象与一次函数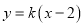 的图象交点为
的图象交点为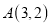 ,
,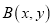 .
.(1)求反比例函数与一次函数的解析式及
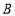 点坐标;
点坐标;(2)若
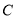 是
是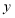 轴上的点,且满足
轴上的点,且满足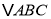 的面积为10,求
的面积为10,求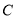 点坐标.
点坐标.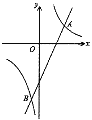
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
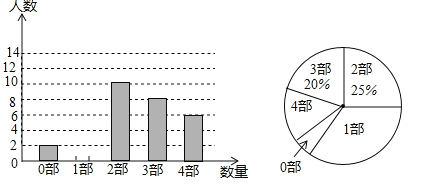
(1)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1部”所在扇形的圆心角为 度.
(2)请将条形统计图补充完整;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)【问题发现】
如图1,在Rt△ABC中,AB=AC=2,∠BAC=90°,点D为BC的中点,以CD为一边作正方形CDEF,点E恰好与点A重合,则线段BE与AF的数量关系为
(2)【拓展研究】
在(1)的条件下,如果正方形CDEF绕点C旋转,连接BE,CE,AF,线段BE与AF的数量关系有无变化?请仅就图2的情形给出证明;
(3)【问题发现】
当正方形CDEF旋转到B,E,F三点共线时候,直接写出线段AF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 经过
经过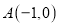 ,
, 两点,且与
两点,且与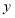 轴交于点
轴交于点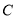 ,点
,点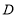 是抛物线的顶点,抛物线的对称轴
是抛物线的顶点,抛物线的对称轴 交
交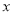 轴于点
轴于点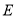 ,连接
,连接 .
.(1)求经过
 ,
,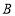 ,
,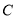 三点的抛物线的函数表达式;
三点的抛物线的函数表达式;(2)点
 是线段
是线段 上一点,当
上一点,当 时,求点
时,求点 的坐标;
的坐标;(3)在(2)的条件下,过点
 作
作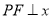 轴于点
轴于点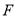 ,
, 为抛物线上一动点,
为抛物线上一动点, 为
为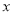 轴上一动点,
轴上一动点, 为直线
为直线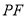 上一动点,当以
上一动点,当以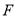 、
、 、
、 、
、 为顶点的四边形是正方形时,请求出点
为顶点的四边形是正方形时,请求出点 的坐标.
的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4),点P是对角线OB上一个动点,点D的坐标为(0,﹣2),当DP与AP之和最小时,点P的坐标为_____.

相关试题

