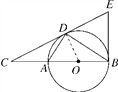
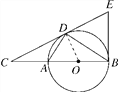
【题目】(2016·西宁中考)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() ,求BE的长.
,求BE的长.

参考答案:
【答案】(1)见解析 (2)![]()
(1)证明:连接OD.∵OB=OD,∴∠OBD=∠BDO.∵∠CDA=∠CBD,∴∠CDA=∠ODB.又∵AB是⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,∴∠ADO+∠CDA=90°,即∠CDO=90°,∴OD⊥CD.∵OD是⊙O的半径,∴CD是⊙O的切线;
(2)解:∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD,∴![]() =
=![]() .∵
.∵![]() =
=![]() ,BC=6,∴CD=4.∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC,∴BE2+BC2=EC2,即BE2+62=(4+BE)2,解得BE=
,BC=6,∴CD=4.∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC,∴BE2+BC2=EC2,即BE2+62=(4+BE)2,解得BE=![]() .
.
【解析】试题分析:连接OD.根据圆周角定理得到∠ADO+∠ODB=90°,
而∠CDA=∠CBD,∠CBD=∠BDO.于是∠ADO+∠CDA=90°,可以证明是切线.
![]() 根据已知条件得到
根据已知条件得到![]() 由相似三角形的性质得到
由相似三角形的性质得到![]() 求得
求得![]() 由切线的性质得到
由切线的性质得到![]() 根据勾股定理列方程即可得到结论.
根据勾股定理列方程即可得到结论.
试题解析:(1)连接OD.
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,即∠CDO=90°,
∴OD⊥CD.
∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD,
![]()
![]() BC=6,∴CD=4.
BC=6,∴CD=4.
∵CE,BE是⊙O的切线,
∴BE=DE,BE⊥BC,
∴BE2+BC2=EC2,
即BE2+62=(4+BE)2,
解得BE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·宁夏中考)如图,已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=2
 ,求CD的长.
,求CD的长.
-
科目: 来源: 题型:
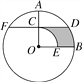
查看答案和解析>>【题目】(2016·新疆中考)如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=
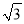 ,以O为圆心,OC为半径作弧CE,交OB于E点.
,以O为圆心,OC为半径作弧CE,交OB于E点.(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B都是五次多项式,则A﹣B一定是( )
A.四次多项式
B.五次多项式
C.十次多项式
D.不高于五次的多项式 -
科目: 来源: 题型:
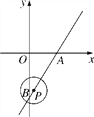
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=
 x-2
x-2 与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.(1)判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3)当⊙P与x轴相切时,求出切点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P先向左平移1个单位,再向上平移2个单位,所得的点为Q(-2,1),则P的坐标为( )
A. (-3,-1) B. (-3,3) C. (-1,-1) D. (-1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线
 ,点
,点 、
、 分别在直线
分别在直线 ,
, 上,点
上,点 为平面内一点.
为平面内一点.(
 )如图,
)如图, ,
, ,
, 的数量关系是__________.
的数量关系是__________.
(
 )利用(
)利用( )的结论解决问题:如图,已知
)的结论解决问题:如图,已知 ,
, 平分
平分 ,
, 平分
平分 ,
, ,求
,求 得度数.
得度数.
(
 )如图,点
)如图,点 为
为 上一点,
上一点, ,
, ,
, 交
交 于点
于点 ,直接写出
,直接写出 ,
, ,
, 之间的数量关系.(用含
之间的数量关系.(用含 的式子表示)
的式子表示)
相关试题

