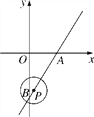
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
与x轴、y轴分别交于A,B两点,P是直线AB上一动点,⊙P的半径为1.
(1)判断原点O与⊙P的位置关系,并说明理由;
(2)当⊙P过点B时,求⊙P被y轴所截得的劣弧的长;
(3)当⊙P与x轴相切时,求出切点的坐标.
参考答案:
【答案】(1)原点O在⊙P外 (2)![]() (3)
(3)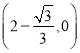 或
或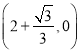
解:(1)原点O在⊙P外.理由如下:∵直线y=![]() x-2
x-2![]() 与x轴、y轴分别交于A,B两点,∴点A的坐标为(2,0),点B的坐标为(0,-2
与x轴、y轴分别交于A,B两点,∴点A的坐标为(2,0),点B的坐标为(0,-2![]() ).在Rt△OAB中,tan∠OBA=
).在Rt△OAB中,tan∠OBA=![]() =
=![]() =
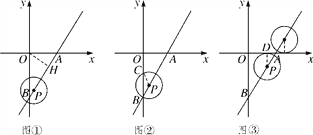
=![]() ,∴∠OBA=30°.如图①,过点O作OH⊥AB于点H,在Rt△OBH中,OH=OB·sin∠OBA=
,∴∠OBA=30°.如图①,过点O作OH⊥AB于点H,在Rt△OBH中,OH=OB·sin∠OBA=![]() .∵
.∵![]() >1,∴原点O在⊙P外;
>1,∴原点O在⊙P外;
(2)如图②,当⊙P过点B时,点P在y轴右侧时,∵PB=PC,∴∠PCB=∠OBA=30°,∴⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,∴弧长为![]() =
=![]() ;同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为
;同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为![]() .∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为
.∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为![]() ;
;
(3)如图③,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,作PD⊥x轴,∴PD∥y轴,∴∠APD=∠ABO=30°.在Rt△DAP中,AD=DP·tan∠DPA=1×tan30°=![]() ,∴OD=OA-AD=2-
,∴OD=OA-AD=2-![]() ,∴此时点D的坐标为
,∴此时点D的坐标为![]() ;当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为
;当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为![]() .综上所述,当⊙P与x轴相切时,切点的坐标为
.综上所述,当⊙P与x轴相切时,切点的坐标为![]() 或
或![]() .
.

【解析】试题分析: ![]() 由直线
由直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,可求得点
两点,可求得点![]() 与点
与点![]() 的坐标,继而求得∠OBA=30°.然后过点O作OH⊥AB于点H,利用三角函数可求得
的坐标,继而求得∠OBA=30°.然后过点O作OH⊥AB于点H,利用三角函数可求得![]() 的长,继而求得答案;
的长,继而求得答案;
![]() 当⊙P过点B时,点P在y轴右侧时,⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,则可求得弧长;同理可求得⊙P过点B时,点P在y轴左侧时, ⊙P被y轴所截的劣弧的长;
当⊙P过点B时,点P在y轴右侧时,⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,则可求得弧长;同理可求得⊙P过点B时,点P在y轴左侧时, ⊙P被y轴所截的劣弧的长;
![]() 首先求得⊙P与x轴相切时,且位于x轴下方时,设切点为D,求出点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
首先求得⊙P与x轴相切时,且位于x轴下方时,设切点为D,求出点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
试题解析:(1)原点O在⊙P外.
理由如下:∵直线![]() 与x轴、y轴分别交于A,B两点,
与x轴、y轴分别交于A,B两点,
∴点A的坐标为(2,0),点B的坐标为![]()
在Rt△OAB中, ![]()
∴∠OBA=30°.
如图①,过点O作OH⊥AB于点H,
在Rt△OBH中, ![]()
![]() ∴原点O在⊙P外;
∴原点O在⊙P外;
(2)如图②,当⊙P过点B时,点P在y轴右侧时,
∵PB=PC,∴∠PCB=∠OBA=30°,
∴⊙P被y轴所截的劣弧所对的圆心角的度数为180°-30°-30°=120°,
∴弧长为: ![]()
同理:当⊙P过点B时,点P在y轴左侧时,弧长同样为![]()
∴当⊙P过点B时,⊙P被y轴所截得的劣弧的长为![]()
(3)如图③,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,作PD⊥x轴,∴PD∥y轴,∴∠APD=∠ABO=30°.
在Rt△DAP中, ![]()
![]()
∴此时点D的坐标为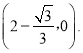
当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为
综上所述,当⊙P与x轴相切时,切点的坐标为 或
或 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·新疆中考)如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=
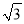 ,以O为圆心,OC为半径作弧CE,交OB于E点.
,以O为圆心,OC为半径作弧CE,交OB于E点.(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B都是五次多项式,则A﹣B一定是( )
A.四次多项式
B.五次多项式
C.十次多项式
D.不高于五次的多项式 -
科目: 来源: 题型:
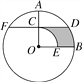
查看答案和解析>>【题目】(2016·西宁中考)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,
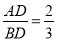 ,求BE的长.
,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,点P先向左平移1个单位,再向上平移2个单位,所得的点为Q(-2,1),则P的坐标为( )
A. (-3,-1) B. (-3,3) C. (-1,-1) D. (-1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:直线
 ,点
,点 、
、 分别在直线
分别在直线 ,
, 上,点
上,点 为平面内一点.
为平面内一点.(
 )如图,
)如图, ,
, ,
, 的数量关系是__________.
的数量关系是__________.
(
 )利用(
)利用( )的结论解决问题:如图,已知
)的结论解决问题:如图,已知 ,
, 平分
平分 ,
, 平分
平分 ,
, ,求
,求 得度数.
得度数.
(
 )如图,点
)如图,点 为
为 上一点,
上一点, ,
, ,
, 交
交 于点
于点 ,直接写出
,直接写出 ,
, ,
, 之间的数量关系.(用含
之间的数量关系.(用含 的式子表示)
的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·滨州中考)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
相关试题

