【题目】如图是二次函数y=ax2+bx+c的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(﹣ ![]() ),(
),( ![]() )是抛物线上两点,则y1<y2其中结论正确的是( )
)是抛物线上两点,则y1<y2其中结论正确的是( ) 
A.①②
B.②③
C.②④
D.①③④
参考答案:
【答案】C
【解析】解:∵抛物线开口向下, ∴a<0,
∵抛物线的对称轴为直线x=﹣ ![]() =1,
=1,
∴b=﹣2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵b=﹣2a,
∴2a+b=0,所以②正确;
∵抛物线与x轴的一个交点为(﹣1,0),抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(3,0),
∴当x=2时,y>0,
∴4a+2b+c>0,所以③错误;
∵点(﹣ ![]() )到对称轴的距离比点(
)到对称轴的距离比点( ![]() )对称轴的距离远,
)对称轴的距离远,
∴y1<y2 , 所以④正确.
故选C.
由抛物线开口方向得到a<0,有对称轴方程得到b=﹣2a>0,由∵抛物线与y轴的交点位置得到c>0,则可对①进行判断;由b=﹣2a可对②进行判断;利用抛物线的对称性可得到抛物线与x轴的另一个交点为(3,0),则可判断当x=2时,y>0,于是可对③进行判断;通过比较点(﹣ ![]() )与点(
)与点( ![]() )到对称轴的距离可对④进行判断.
)到对称轴的距离可对④进行判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元. 经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元)
…
70
90
…
销售量y(件)
…
3000
1000
…
(利润=(售价﹣成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40000元? -
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,如图①所示,∠BAB′=θ,
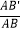 =
=  =
=  =n,我们将这种变换记为[θ,n].
=n,我们将这种变换记为[θ,n].
(1)如图①,对△ABC作变换[60°, ]得到△AB′C′,则S△AB'C:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
]得到△AB′C′,则S△AB'C:S△ABC=;直线BC与直线B′C′所夹的锐角为度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、C′在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.随机抛掷一枚硬币,反面一定朝上
B.数据3,3,5,5,8的众数是8
C.某商场抽奖活动获奖的概率为 ,说明毎买50张奖券中一定有一张中奖
,说明毎买50张奖券中一定有一张中奖
D.想要了解广安市民对“全面二孩”政策的看法,宜采用抽样调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=3,AD=4
 ,AF交BC于E,交DC的延长线于F,且CF=1,则CE的长为 .
,AF交BC于E,交DC的延长线于F,且CF=1,则CE的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣
 )﹣2﹣(π﹣
)﹣2﹣(π﹣  )0﹣|
)0﹣|  ﹣2|+2sin60°.
﹣2|+2sin60°. -
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,点E、F分别在AB、CD上,且AE=CF.

(1)求证:△ADE≌△CBF;
(2)若DF=BF,求证:四边形DEBF为菱形.
相关试题

