【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.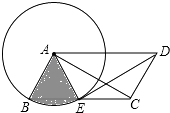
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴四边形AECD是梯形,
∵AB=AE,
∴AE=CD,
∴四边形AECD是等腰梯形,
∴AC=DE,
在△AED和△DCA中,
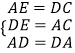 ,
,
∴△AED≌△DCA(SSS)
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵四边形AECD是等腰梯形,
∴∠DAE=∠ADC=2∠ADE,
∵DE与⊙A相切于点E,
∴AE⊥DE,
即∠AED=90°,
∴∠ADE=30°,
∴∠DAE=60°,
∴∠DCE=∠AEC=180°﹣∠DAE=120°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠DCE=120°,
∴∠BAE=∠BAD﹣∠EAD=60°,
∴S阴影= ![]() ×π×22=
×π×22= ![]() π.
π.
【解析】(1)利用平行四边形的性质和等腰梯形的判定与性质可证得全等;(2)由切线的性质定理和等腰梯形的性质、平行四边形的性质求出阴影扇形的圆心角度数,进而求出面积.
【考点精析】利用平行四边形的性质和切线的性质定理对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知: 用 2 辆
 型车和 1 辆
型车和 1 辆 型车载满货物一次可运货 10 吨; 用 1 辆
型车载满货物一次可运货 10 吨; 用 1 辆 型车和 2 辆
型车和 2 辆 型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:
型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:(1) 1 辆
 型车和 1 辆
型车和 1 辆 型车载满货物一次可分别运货多少吨?
型车载满货物一次可分别运货多少吨?(2) 某物流公司现有货物若干吨要运输, 计划同时租用
 型车 6 辆,
型车 6 辆, 型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输?
型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把抛物线y=
 x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=  x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
 坐标为
坐标为 ,点
,点 的坐标为
的坐标为 .
.(1)求直线
 的解析式;
的解析式;(2)点
 是坐标轴上的一个点,若
是坐标轴上的一个点,若 为直角边构造直角三角形
为直角边构造直角三角形 ,请求出满足条件的所有点
,请求出满足条件的所有点 的坐标;
的坐标;(3)如图 2,以点
 为直角顶点作
为直角顶点作 ,射线
,射线 交
交 轴的负半轴与点
轴的负半轴与点 ,射线
,射线 交
交 轴的负半轴与点
轴的负半轴与点 ,当
,当 绕点
绕点 旋转时,
旋转时, 的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程) .
的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是
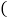
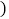
A. 当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B. 当M,N,P,Q是各边中点,且
 时,四边形MNPQ为正方形
时,四边形MNPQ为正方形C. 当M,N、P,Q是各边中点,且
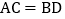 时,四边形MNPQ为菱形
时,四边形MNPQ为菱形D. 当M,N、P、Q是各边中点,且
 时,四边形MNPQ为矩形
时,四边形MNPQ为矩形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
相关试题

