【题目】今年秋季,斗门土特产喜获丰收,某土特产公司组织10辆汽车装运甲,乙,丙三种土特产去外地销售,按计划10辆车都要装运,每辆汽车只能装运同一士特产,且必须装满,设装运甲种士特产的汽车有x辆,装运乙种特产的汽车有y辆,根据下表提供的信息,解答以下问题:
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量(吨) | 4 | 3 | 6 |
每吨土特产获利(元) | 1000 | 900 | 1600 |
(1)装运丙种土特产的车辆数为 辆(用含有x,y的式子表示);
(2)用含有x,y的式子表示这10辆汽车共装运土特产的数量;
(3)求销售完装运的这批土特产后所获得的总利润(用含有x,y的式子表示).
参考答案:
【答案】(1)(10﹣x﹣y);(2)(60﹣2x﹣3y)吨;(3)(96000﹣5600x﹣6900y)元.
【解析】
(1)根据“装运丙种土特产的车辆数![]() 总汽车辆数
总汽车辆数![]() 装运甲种土特产的车辆数
装运甲种土特产的车辆数![]() 装运乙种土特产的车辆数”列式表达便可;
装运乙种土特产的车辆数”列式表达便可;
(2)根据“装运甲种土特产的每辆车运载重量![]() 装运甲种土特产的车辆数
装运甲种土特产的车辆数![]() 装运乙种土特产的每辆车运载重量
装运乙种土特产的每辆车运载重量![]() 装运乙种土特产的车辆数
装运乙种土特产的车辆数![]() 装运丙种土特产的每辆车运载重量
装运丙种土特产的每辆车运载重量![]() 装运丙种土特产的车辆数
装运丙种土特产的车辆数![]() 辆汽车共装运土特产的数量”列出代数式并化简便可;
辆汽车共装运土特产的数量”列出代数式并化简便可;
(3)根据“甲种土特产每吨利润![]() 甲种土特产的总吨数
甲种土特产的总吨数![]() 乙种土特产每吨利润
乙种土特产每吨利润![]() 乙种土特产的总吨数
乙种土特产的总吨数![]() 丙种土特产每吨利润
丙种土特产每吨利润![]() 丙种土特产的总吨数
丙种土特产的总吨数![]() 总利润”列出代数式,并化简便可.
总利润”列出代数式,并化简便可.
解:(1)由题意得,
装运丙种土特产的车辆数为:![]() (辆
(辆![]()
故答案为:![]() ;
;
(2)根据题意得,
![]()
![]()
![]() ,
,
答:这10辆汽车共装运土特产的数量为![]() 吨;
吨;
(3)根据题意得,
![]()
![]()
![]()
答:销售完装运的这批土特产后所获得的总利润为![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
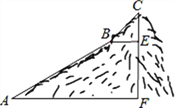
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(
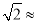 1.414,CF结果精确到米)
1.414,CF结果精确到米) -
科目: 来源: 题型:
查看答案和解析>>【题目】一种股票第一天的最高价比开盘价高0.3元,最低价比开盘价低0.2元;第二天的最高价开盘价高0.2元,最低价比开盘价低0.1元;第三天的最高价等于开盘价,最低价比开盘价低0.13元.计算每天最高价与最低价的差,以及这些差的平均值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,AC垂直平分BD,交BD于点F,延长DC到点E,使得CE=DC,连接BE.
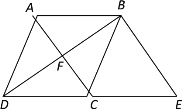
(1)求证:四边形ABCD是菱形.
(2)填空:
①当∠ADC= °时,四边形ACEB为菱形;
②当∠ADC=90°,BE=4时,则DE=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店,准备用不超过2800元购买足球和篮球共计60个,已知一个篮球的进价为50元,售价为65元;一个足球的进价为40元,售价为50元.
(1)若购进x个篮球,购买这批球共花费y元,求y与x之间的函数关系式;
(2)设售出这批球共盈利w元,求w与x之间的函数关系式;
(3)体育用品商店购进篮球和足球各多少个时,才能获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
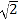 ≈1.4,
≈1.4, 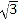 ≈1.7).
≈1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班去商场为书法比赛买奖品,书包每个定价40元,文具盒每个定价8元,商场实行两种优惠方案:①买一个书包送一个文具盒:②按总价的9折付款.若该班需购买书包10个,购买文具盒若干个(不少于10个).
(1)当买文具盒40个时,分别计算两种方案应付的费用;
(2)当购买文具盒多少个时,两种方案所付的费用相同;
(3)如何根据购买文具盒的个数,选择哪种优惠方案的费用比较合算?
相关试题

