搜索
【题目】计算或化简：
（1）
（2）
（3）4×(－
)+(－2)2×5－4÷(－
)； （4）
（5）
（6）
参考答案：
【答案】（1）10；（2）2；（3）28；（4）-1；（5）
；（6）
；
【解析】
（1）先化简再计算加减法；
（2）利用加法交换律和加法结合律矩形简便运算；
（3）先算乘方和乘除，再算加减；
（4）根据有理数的混合运算，顺序，先乘方，再乘除，最后算加减解答即可；
（5）根据整式的运算法则即可求出答案；
（6）根据整式的混合计算顺序解答即可．
（1）原式=-8+15-9+12=-17+27=10；
（2）原式=-1.5-8.5+1.25+10.25=-10+12=2；
（3）原式=-
+4×5-4×(－
)= -+20+
=20+8=28；
（4）原式=(4
×36+
×36
×36)÷5=（-4-28+33-6）÷5=-5÷5=-1；
（5）原式=
=-a+
；
（6）原式=15a2b-5ab2+4ab2-12a2b=3a2b-ab2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，是抛物线形拱桥，当拱顶离水面2米时，水面宽4米．若水面下降1米，则水面宽度将增加多少米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为⊙O的直径，点F为弦AC的中点，连接OF并延长交⊙O于点D，过点D作⊙O的切线，交BA的延长线于点E．
（1）求证：AC∥DE；
（2）若OA=AE=4，求AC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”．
（1）请写出两个为“同簇二次函数”的函数；
（2）已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5，其中y1的图象经过点A（1，1），若y1+y2与y1为“同簇二次函数”，求函数y2的表达式，并求出当0≤x≤3时，y2的最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，抛物线y=﹣2x2+（m+9）x﹣6的对称轴是x=2．
（1）求抛物线表达式和顶点坐标；
（2）将该抛物线向右平移1个单位，平移后的抛物线与原抛物线相交于点A，求点A的坐标；
（3）抛物线y=﹣2x2+（m+9）x﹣6与y轴交于点C，点A关于平移后抛物线的对称轴的对称点为点B，两条抛物线在点A、C和点A、B之间的部分（包含点A、B、C） 记为图象M．将直线y=2x﹣2向下平移b（b＞0）个单位，在平移过程中直线与图象M始终有两个公共点，请你写出b的取值范围 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场将进货价为40元的台灯以50元的销售价售出，平均每月能售出800个．市场调研表明：当销售价每上涨1元时，其销售量就将减少10个．若设每个台灯的销售价上涨
元．（1）试用含
的代数式填空：①涨价后，每个台灯的销售价为 元；
②涨价后，商场的台灯平均每月的销售量为 台；
③涨价后，商场每月销售台灯所获得总利润为 元．
（2）如果商场要想销售总利润平均每月达到20000元，商场经理甲说“在原售价每台50元的基础上再上涨40元，可以完成任务”，商场经理乙说“不用涨那么多，在原售价每台50元的基础上再上涨30元就可以了”，试判断经理甲与乙的说法是否正确，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读资料：
如图1，在平面直角坐标系xOy中，A，B两点的坐标分别为A（x1 ， y1），B（x2 ， y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 ， 所以A，B两点间的距离为AB=
．
我们知道，圆可以看成到圆心的距离等于半径的点的集合，如图2，在平面直角坐标系xOy中，A （x，y）为圆上任意一点，则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 ， 当⊙O的半径OA为r时，⊙O的方程可写为：x2+y2=r2 ．
问题拓展：
如果圆心坐标为P （a，b），半径为r，那么⊙P的方程可以写为 （x﹣a）2+（y﹣b）2=r2 ．
综合应用：
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使∠POA=30°，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
①证明AB是⊙P的切线；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以点Q为圆心，OQ长为半径的⊙Q的方程；若不存在，说明理由．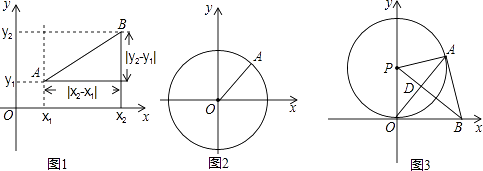
相关试题
