【题目】阅读资料:
如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB= ![]() .
.
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.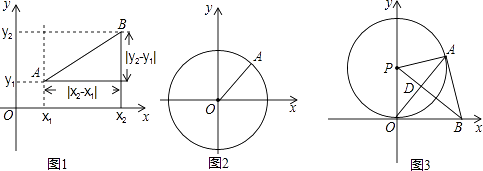
参考答案:
【答案】解:问题拓展:设A(x,y)为⊙P上任意一点,
∵P(a,b),半径为r,
∴AP2=(x﹣a)2+(y﹣b)2=r2 .
故答案为:(x﹣a)2+(y﹣b)2=r2;
综合应用:
①∵PO=PA,PD⊥OA,
∴∠OPD=∠APD.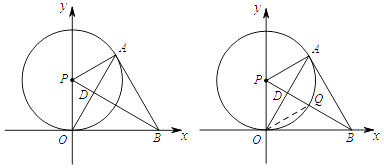
在△POB和△PAB中, 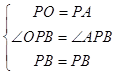 ,
,
∴△POB≌△PAB.
∴∠PAB=∠POB=90°.
∴PA⊥AB.
∵PA是半径,PA⊥AB于A,
∴AB是⊙P的切线.
②存在到四点O,P,A,B距离都相等的点Q.
当点Q在线段BP中点时,
∵∠POB=∠PAB=90°,
∴QO=QP=QA=QB.
∴此时点Q到四点O,P,A,B距离都相等.
∵PB⊥OA,∠POB=90°,∠POA=30°,
∴∠PBO=30°.
∴在Rt△POB中, ![]() ,PB=2PO=12.
,PB=2PO=12.
∴B点坐标为 ![]() .
.
∵Q是PB中点,P(0,6),B ![]() ,
,
∴Q点坐标为 ![]() .
.
∵ ![]() ,
,
∴以Q为圆心,OQ为半径的⊙Q的方程为 ![]()
【解析】问题拓展:设A(x,y)为⊙P上任意一点,则有AP=r,根据阅读材料中的两点之间距离公式即可求出⊙P的方程;
综合应用:①由PO=PA,PD⊥OA可得∠OPD=∠APD,从而可证到△POB≌△PAB,则有∠POB=∠PAB.由⊙P与x轴相切于原点O可得∠POB=90°,即可得到∠PAB=90°,由此可得AB是⊙P的切线;
②当点Q在线段BP中点时,根据直角三角形斜边上的中线等于斜边的一半可得QO=QP=BQ=AQ.易证∠OBP=∠POA=30°.由P点坐标可求出OP、OB.过点Q作QH⊥OB于H,易证△BHQ∽△BOP,根据相似三角形的性质可求出QH、BH,进而求出OH,就可得到点Q的坐标,然后运用问题拓展中的结论就可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)
 (2)
(2)
(3)4×(-
 )+(-2)2×5-4÷(-
)+(-2)2×5-4÷(-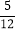 ); (4)
); (4)
(5)
 (6)
(6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2.
(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
(3)抛物线y=﹣2x2+(m+9)x﹣6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C) 记为图象M.将直线y=2x﹣2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进货价为40元的台灯以50元的销售价售出,平均每月能售出800个.市场调研表明:当销售价每上涨1元时,其销售量就将减少10个.若设每个台灯的销售价上涨
 元.
元.(1)试用含
 的代数式填空:
的代数式填空:①涨价后,每个台灯的销售价为 元;
②涨价后,商场的台灯平均每月的销售量为 台;
③涨价后,商场每月销售台灯所获得总利润为 元.
(2)如果商场要想销售总利润平均每月达到20000元,商场经理甲说“在原售价每台50元的基础上再上涨40元,可以完成任务”,商场经理乙说“不用涨那么多,在原售价每台50元的基础上再上涨30元就可以了”,试判断经理甲与乙的说法是否正确,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示.
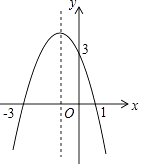
(1)求这个二次函数的解析式;
(2)根据图象,写出当x取何值时,y>0? -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.

相关试题

