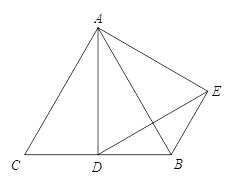
【题目】如图,在等边△ABC中,点D为边BC的中点,以AD为边作等边△ADE,连接BE.求证:BE=BD
参考答案:
【答案】证明见解析.
【解析】根据等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=AC,AD=DE=AE,进而就可以得出△ABD≌△ACE.
证明:∵在等边△ABC中,点D为边BC的中点,
∴∠CAD =∠DAB=![]() ∠CAB= 30°,
∠CAB= 30°,
∵△ADE为等边三角形,
∴AD=AE,∠DAE= 60°,
∵∠DAB= 30°,
∴∠DAB =∠EAB= 30°,
在△ADB与△AEB中,
∴△ADB≌△AEB,
∴ BE=BD.
“点睛”本题考查了等边三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,两对角线交于点O,则图中面积相等的三角形有( ).

A.4对
B.3对
C.2对
D.1对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;
若点P在直线x = 2上,则点P关于⊙O的最大“视角”的度数 ;
②在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标;
③若点P在直线
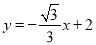 上,且点P关于⊙O的“视角”大于60°,求点P的横坐标
上,且点P关于⊙O的“视角”大于60°,求点P的横坐标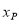 的取值范围.
的取值范围.(2)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,-1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标
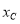 的取值范围.
的取值范围.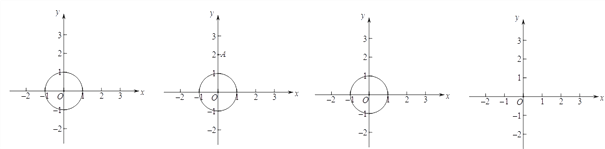
-
科目: 来源: 题型:
查看答案和解析>>【题目】能说明△ABC≌△DEF的条件是( )
A.AB=DE,AC=DF,∠C=∠F
B.AC=EF,∠A=∠D,∠B=∠E
C.AB=DE,BC=EF,∠A=∠D
D.BC=EF,AB=DE,∠B=∠E
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;

(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
-
科目: 来源: 题型:
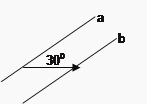
查看答案和解析>>【题目】把直线a沿箭头方向平移1.5cm得直线b,这两条直线之间的距离是( )
A.1.5cm
B.3cm
C.0.75cm
D.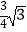 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】第二象限内的点P(x,y)满足|x|=5,y2=4,则点P的坐标是____________;
相关试题

