
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 相交于点
相交于点![]() ,
,![]() .
.
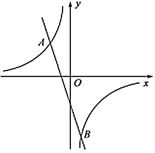
(1)求出直线![]() 的表达式;
的表达式;
(2)在![]() 轴上有一点
轴上有一点![]() 使得
使得![]() 的面积为18,求出点
的面积为18,求出点![]() 的坐标.
的坐标.
科目:初中数学 来源: 题型:
【题目】如图1,草原上有A,B,C三个互通公路的奶牛养殖基地,B与C之间距离为100千米,C在B的正北方,A在C的南偏东60°方向且在B的北偏东30°方向.A地每年产奶3万吨;B地有奶牛9000头,平均每头牛的年产奶量为3吨;C地养了三种奶牛,其中黑白花牛的头数占20%,三河牛的头数占35%,其他情况反映在图(2),图(3)中.

(1)通过计算补全图(3);
(2)比较B地与C地中,哪一地平均每头牛的年产奶量更高?
(3)如果从B,C两地中选择一处建设一座工厂解决三个基地的牛奶加工问题,当运送一吨牛奶每千米的费用都为1元,那么从节省运费的角度考虑,应在何处建设工厂?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在防疫工作稳步推进的过程中,复工复产工作也在如火如荼进行.某企业计划通过扩大生产能力来消化第一季度积累的订单,决定增加一条新的生产线并招收工人.根据以往经验,一名熟练工人每小时完成的工件数量比一名普通工人每小时完成的工件数量多10个,且一名熟练工人完成160个工件与一名普通工人完成80个工件所用的时间相同.
(1)求一名熟练工人和一名普通工人每小时分别能完成多少个工件;
(2)新生产线的目标产能是每小时生产200个工件,计划招聘![]() 名普通工人与
名普通工人与![]() 名熟练工人共同完成这项任务,请写出
名熟练工人共同完成这项任务,请写出![]() 与
与![]() 的函数关系式(不需要写自变量
的函数关系式(不需要写自变量![]() 的取值范围);
的取值范围);
(3)该企业在做市场调研时发现,一名普通工人每天工资为120元,一名熟练工人每天工资为150元,而且本地区现有熟练工人不超过8人.在(2)的条件下,该企业如何招聘工人,使得工人工资的总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交边
的角平分线交边![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上以每秒
上以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向从点
方向从点![]() 开始运动,过点
开始运动,过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边向右作平行四边形
为边向右作平行四边形![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() ,设
,设![]() 点运动时间为
点运动时间为![]() 秒.
秒.
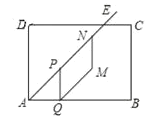
(1)![]() ____________(用含
____________(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与矩形
与矩形![]() 重合部分面积为
重合部分面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)直接写出在点![]() 、
、![]() 运动的过程中,整个图形中形成的三角形存在全等三角形时
运动的过程中,整个图形中形成的三角形存在全等三角形时![]() 的值(不添加任何辅助线).
的值(不添加任何辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
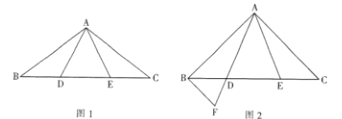
【题目】已知,在![]() 中,
中,![]() ,点D,点E在BC上,
,点D,点E在BC上,![]() ,连接
,连接![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,过点B作
时,过点B作![]() ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.
(1)求证:PB是⊙O的切线;
(2)若cos∠PAB=![]() ,BC=2,求PO的长.
,BC=2,求PO的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com