
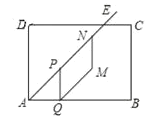
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交边
的角平分线交边![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上以每秒
上以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向从点
方向从点![]() 开始运动,过点
开始运动,过点![]() 作
作![]() 于点
于点![]() ,以
,以![]() 为边向右作平行四边形
为边向右作平行四边形![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() ,设
,设![]() 点运动时间为
点运动时间为![]() 秒.
秒.
(1)![]() ____________(用含
____________(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 上时,求
上时,求![]() 的值;
的值;
(3)设平行四边形![]() 与矩形
与矩形![]() 重合部分面积为
重合部分面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,求
上运动时,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)直接写出在点![]() 、
、![]() 运动的过程中,整个图形中形成的三角形存在全等三角形时
运动的过程中,整个图形中形成的三角形存在全等三角形时![]() 的值(不添加任何辅助线).
的值(不添加任何辅助线).
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3) ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)判断出![]() 等腰直角三角形即可得出结论;
等腰直角三角形即可得出结论;
(2)先判断出点Q是AB中点,进而求出AQ=4,即可得出结论;
(3)分三种情况进行讨论:①如图4中,当![]()
![]() 时,重叠部分是平行四边形PQMN,②如图5中,当
时,重叠部分是平行四边形PQMN,②如图5中,当![]() ,重叠部分是五边形PQMGE,③如图6中,
,重叠部分是五边形PQMGE,③如图6中,![]() 时,重叠部分是五边形PQGCE,延长QP交CD于K,分别求解即可.
时,重叠部分是五边形PQGCE,延长QP交CD于K,分别求解即可.
(4)分三种情况讨论即可:①如图7中,当Q时AB中点时,![]() ,②如图8中,当点P与点E重合时,
,②如图8中,当点P与点E重合时,![]() ,③如图9中,当
,③如图9中,当![]() 时,分别求解即可.
时,分别求解即可.
(1)∵四边形ABCD是矩形,
∴![]() ,
,
∵AE是![]() 的角平分线,
的角平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
即![]() 是等腰直角三角形,
是等腰直角三角形,
由运动知,![]() ,
,
∴![]() ,
,
故答案为t.
(2)如图,
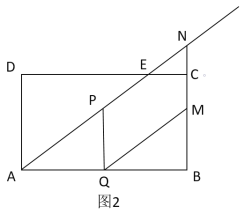
∵四边形PQMN是平行四边形,
∴![]() ,
,
∵点M在BC上,
∴![]() ,
,
∵AP=PN,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
由运动知,![]()
∴![]() ,
,
∴![]() .
.
(3)①如图4所示,当![]() 时,重叠部分是平行四边形PQMN,
时,重叠部分是平行四边形PQMN,![]() ,
,
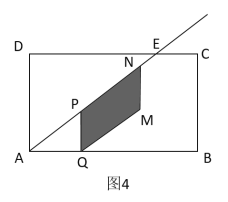
②如图5所示,
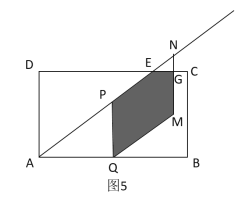
当![]() ,重叠部分是五边形PQMGE,
,重叠部分是五边形PQMGE,
∴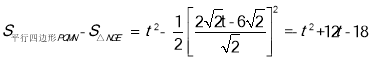 .
.
③如图6,
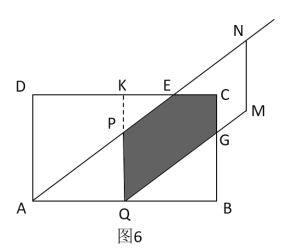
当![]() ,重叠部分是五边形PQGCE,延长QP交CD于K,
,重叠部分是五边形PQGCE,延长QP交CD于K,
∴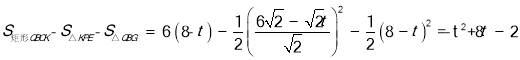 .
.
综上所述: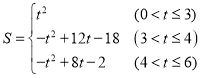 .
.
(4)①如图7中,
当点Q是AB中点时,![]() ,此时
,此时![]() .
.
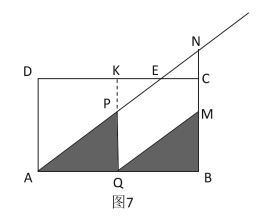
②如图8中,
当点P与点E重合时,![]() ,此时
,此时![]() .
.
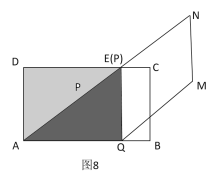
③如图9,
当![]() 时,由EK=BQ得到,
时,由EK=BQ得到,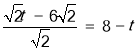 ,解得
,解得![]() .
.
综上所述,![]() 或
或![]() 或
或![]() 时,整个图形中形成的三角形存在全等三角形.
时,整个图形中形成的三角形存在全等三角形.


科目:初中数学 来源: 题型:
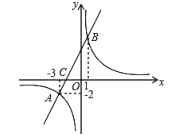
【题目】如图,一次函数![]() 图象与反比例函数
图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式.
的解析式.
(2)求点![]() 坐标.
坐标.
(3)平面上的点![]() 与点
与点![]() 、
、![]() 、
、![]() 构成平行四边形,请直接写出满足条件的
构成平行四边形,请直接写出满足条件的![]() 点坐标______.
点坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
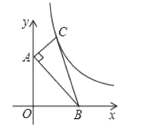
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,点
,点![]() 在第一象限内,
在第一象限内,![]() ,
,![]() ,函数
,函数![]() 的图像经过点
的图像经过点![]() ,将
,将![]() 沿
沿![]() 轴的正方向向右平移
轴的正方向向右平移![]() 个单位长度,使点
个单位长度,使点![]() 恰好落在函数
恰好落在函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位食堂为全体名职工提供了![]() 四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取
四种套餐,为了解职工对这四种套餐的喜好情况,单位随机抽取![]() 名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
名职工进行“你最喜欢哪一种套餐(必选且只选一种)”问卷调查,根据调查结果绘制了条形统计图和扇形统计图,部分信息如下:
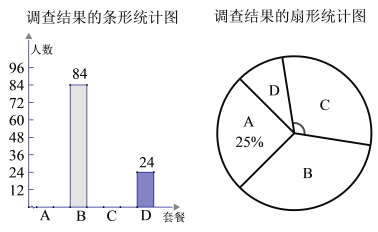
![]() 在抽取的
在抽取的![]() 人中最喜欢
人中最喜欢![]() 套餐的人数为 ,扇形统计图中“
套餐的人数为 ,扇形统计图中“![]() ”对应扇形的圆心角的大小为 ;
”对应扇形的圆心角的大小为 ;
![]() 依据本次调查的结果,估计全体
依据本次调查的结果,估计全体![]() 名职工中最喜欢
名职工中最喜欢![]() 套餐的人数;
套餐的人数;
![]() 现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”,求甲被选到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com