搜索
【题目】用两个全等的等边三角形，可以拼成下列哪种图形（ ）
A.矩形
B.菱形
C.正方形
D.等腰梯形
参考答案：
【答案】B
【解析】由题可知，得到的四边形的四条边也相等，得到的图形是菱形．由于两个等边三角形的边长都相等，则得到的四边形的四条边也相等，即是菱形．故答案为：B．根据菱形的判定定理四边相等的四边形是菱形可判断结果。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果点（m﹣1，﹣1）与点（5，﹣1）关于y轴对称，则m＝（ ）
A.4B.﹣4C.5D.﹣5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB的度数是（ ）
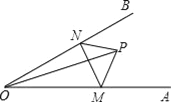
A. 25° B. 30° C. 35° D. 40°
-
科目： 来源： 题型：
查看答案和解析>>【题目】用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是__（写出全等的简写）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．
（1）求证：△ADC≌△CEB．
（2）AD=5cm，DE=3cm，求BE的长度．
-
科目： 来源： 题型：
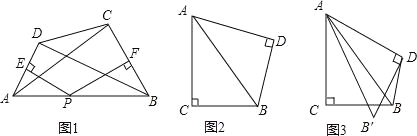
查看答案和解析>>【题目】（1）如图，在四边形ABCD中，AB=AD，∠B=∠D=90°，E、F分别是边BC、CD上的点，且∠EAF=
∠BAD．求证：EF=BE+FD；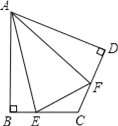
（2）如图，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是边BC、CD上的点，且∠EAF=
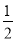∠BAD，（1）中的结论是否仍然成立？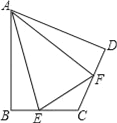
（3）如图，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E、F分别是边BC、CD延长线上的点，且∠EAF=
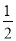∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．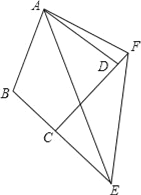
-
科目： 来源： 题型：
查看答案和解析>>【题目】(2016浙江省舟山市第23题)我们定义：有一组邻角相等的凸四边形叫做“等邻角四边形”
（1）概念理解：
请你根据上述定义举一个等邻角四边形的例子；
（2）问题探究；
如图1，在等邻角四边形ABCD中，∠DAB=∠ABC，AD，BC的中垂线恰好交于AB边上一点P，连结AC，BD，试探究AC与BD的数量关系，并说明理由；
（3）应用拓展；
如图2，在Rt△ABC与Rt△ABD中，∠C=∠D=90°，BC=BD=3，AB=5，将Rt△ABD绕着点A顺时针旋转角α（0°＜∠α＜∠BAC）得到Rt△AB′D′（如图3），当凸四边形AD′BC为等邻角四边形时，求出它的面积．
相关试题
