[题目]化简(1)(m-2n)(m2+4n2)(m+2n)(2)(x+2y+z)(x+2y-z) 题目和参考答案 ——青夏教育精英家教网—

【题目】化简

（1）（m-2n）（m2+4n2）（m+2n）

（2）（x+2y+z）（x+2y-z）

参考答案：

【答案】（1）m4-16n4；（2）x2+4xy+4y2-z2

【解析】

（1）原式利用平方差公式计算即可得到结果；

（2）将原式进一步转化为[（x+2y）+z][（x+2y）-z]后，利用平方差公式计算，再利用完全平方公式计算即可．

解：（1）原式=（m2-4n2）（m2+4n2）=m4-16n4；

（2）原式=[（x+2y）+z][（x+2y）-z]=（x+2y）2-z2=x2+4xy+4y2-z2

相关试题

科目： 来源： 题型：

【题目】在平面直角坐标系中，菱形OABC的OC边落在x轴上，∠AOC=60°，OA=60．若菱形OABC内部（边界及顶点除外）的一格点P（x，y）满足：x2﹣y2=90x﹣90y，就称格点P为“好点”，则菱形OABC内部“好点”的个数为（　　）
（注：所谓“格点”，是指在平面直角坐标系中横、纵坐标均为整数的点．）
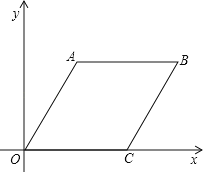
A. 145 B. 146 C. 147 D. 148
查看答案和解析>>
科目： 来源： 题型：

【题目】荣昌公司要将本公司100吨货物运往某地销售，经与春晨运输公司协商，计划租用甲、乙两种型号的汽车共6辆，用这6辆汽车一次将货物全部运走，其中每辆甲型汽车最多能装该种货物16吨，每辆乙型汽车最多能装该种货物18吨．已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元；租用2辆甲型汽车和1辆乙型汽车共需费用2450元，且同一种型号汽车每辆租车费用相同．
（1）求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元？
（2）若荣昌公司计划此次租车费用不超过5000元．通过计算求出该公司有几种租车方案？请你设计出来,并求出最低的租车费用．
查看答案和解析>>
科目： 来源： 题型：

【题目】某中学库存若干套桌椅，准备修理后支援贫困山区学校。现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费。
(1)该中学库存多少套桌椅？
(2)在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案:a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理。你认为哪种方案省时又省钱？为什么？
查看答案和解析>>
科目： 来源： 题型：

【题目】下列命题中，正确的有（）
①Rt△ABC中，已知两边长分别为3和4，则第三边长为5；
②有一个内角等于其他两个内角和的三角形是直角三角形；
③三角形的三边分别为a，b，C，若a2+c2=b2，那么∠C=90°；
④若△ABC中，∠A：∠B：∠C=1：5：6，则△ABC是直角三角形．
A．1个 B．2个 C．3个 D．4个
查看答案和解析>>
科目： 来源： 题型：

【题目】已知如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点BD是对角线，AG∥DB，交CB的延长线于G，连接GF，若AD⊥BD．下列结论：①DE∥BF；②四边形BEDF是菱形；③FG⊥AB；④S△BFG=．其中正确的是（　　）
A. ①②③④ B. ①② C. ①③ D. ①②④
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，矩形ABCD的边BC在x轴上，点A在第二象限，点D在第一象限，AB=2，OD=4，将矩形ABCD绕点O旋转，使点D落在x轴上，则点C对应点的坐标是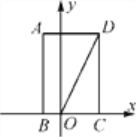
A. (–，1) B. (–1，) C. (–1，)或(1，–) D. (–，1)或(1，–)
查看答案和解析>>