搜索
【题目】如图，平行四边形ABCD中，点E、F分别在AD、AB上，依次连接EB、EC、FC、FD，图中阴影部分的面积分别为S1、S2、S3、S4 ， 已知S1=2、S2=12、S3=3，则S4的值是 ． 
参考答案：
【答案】7
【解析】解：设平行四边形的面积为S，则S△CBE=S△CDF= 
S， 由图形可知，△CDF面积+△CBE面积+（S1+S4+S3）﹣S2=平行四边形ABCD的面积
∴S=S△CBE+S△CDF+2+S4+3﹣12，
即S= S+ S+2+S4+3﹣12，
解得S4=7，
所以答案是：7．
【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列成语所描述的事件，是随机事件的是（ ）
A. 水涨船高 B. 一箭双雕 C. 水中捞月 D. 一步登天
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知|a|=3，b2=16，且|a+b|≠a+b，则代数式a+b的值为（ ）
A.1或7B.1或-7C.-1或-7D.±1或±7
-
科目： 来源： 题型：
查看答案和解析>>【题目】综合与实践：
发现问题：
如图①，已知：△OAB中，OB=3，将△OAB绕点O逆时针旋转90°得△OA′B，连接BB′．
则BB′= ．
问题探究：
如图②，已知△ABC是边长为4
的等边三角形，以BC为边向外作等边△BCD，P为△ABC内一点，将线段CP绕点C逆时针旋转60°，P的对应点为Q．（1）求证：△DCQ≌△BCP
（2）求PA+PB+PC的最小值．
实际应用：
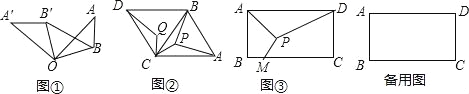
如图③，某货运场为一个矩形场地ABCD，其中AB=500米，AD=800米，顶点A、D为两个出口，现在想在货运广场内建一个货物堆放平台P，在BC边上（含B、C两点）开一个货物入口M，并修建三条专用车道PA、PD、PM．若修建每米专用车道的费用为10000元，当M，P建在何处时，修建专用车道的费用最少？最少费用为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点P是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C，D.
(1)∠PCD＝∠PDC吗？为什么？
(2)OP是CD的垂直平分线吗？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y=-2x+b的图象经过点A(-1,y1)和点B(3,y2),则y1与y2的大小关系为 ( )
A. y1<y2 B. y1>y2 C. y1=y2 D. 不能确定
相关试题
